Math 336, History of Math

I Early Civilizations (3500 B.C. to 500ish B.C.) [Chap. 1 and 2]

A General comments on beginning and evolution of first mathematics

1 Primitive peoples (from 30,000 B.C. on) dealt with early concepts of number
(“one, two , many”), and used tallying (marks on bones, knots in ropes,
pebbles) to handle larger numbers for business and calendar. [Sec. 1.1]

2 Early civilizations, needing to count larger quantities, begin more sophisticated
counting methods, introducing special symbols for numbers [Chp.1].

3 Over time, they developed more mathematics: some primitive arithmetic ,
algebra and geometry, [Chp. 2].

B Babylonians [Sec. 1.3, 2.5]

1 lived in “fertile crescent” of Mesopotamia

2 cuneiform, reed on clay tablets made 2 symbols (Y and >)

3 positional, base 60 number system

4 knew lots of algebra and some geometry: 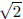= diagonal of unit square,
pythagorean theorem, how to solve quadratic equations , how to solve area vs.
perimeter (xy = a, x + y = b), solving other algebraic equations using tricks
to reduce to problems they knew.

5 no proofs, just word problems with solutions , and tables: listing of squares
and cubes , or Plimpton 322 (1900-1600 B.C.) = table of pythagorean triples.

6 tablets not translated til late 1800s, so we only recently appreciate them.

C Egyptians [Sec. 1.2, 2.1, 2.2, 2.3]

1 lived in thin strip around Nile river

2 papyrus and stylus, hieroglyphics → hieratic → demotic

3 non-positional number system, clunky

4 since big civilization in desert, did practical mathematics

5 multiplication /division by doubling (since numbers to clunky for direct use)

6 unit fractions only , other ratios = sum of unit fractions

7 Rhind Papyrus (1600 B.C.) : “textbook” with all egyptian math explained as
word problems and solutions. Examples: solving linear equations by “false
position”, “think of a number” problems.

8 Rosetta Stone: translation key, with hierogly., demotic, and Greek. Greeks
appreciated Egypt and wrote of them. Napoleaon found R.S., allowed modern
europe to appreciate/understand Egypt even more.

D Chinese [overview of all chinese given in Sec. 1.2, more details in sec. 5.5]

1 base 10, positional numbers by 1400 B.C. at least

2 counting rods used by 1000 B.C.

3 damp climate and wrote on bamboo sheets, so few records exist of early
chinese accomplishments (oldest math text is Nine Chapters, 150 A.D.).

4 mathematics always practial (early → 16th century): business, astronomy

5 during europe’s dark ages, chinese kept going, inventing gunpowder, magnetic
compass, paper and printing, which eventually made it to the west,
passed by the Arabs.

E Mayans of Central America: positional, base 20 number system used to make
fairly accurate astronomial calendar

II Early Greeks (500s to 300s B.C.) [Chp. 3]

A History

1 Ancient Greece emerging 11th–9th century B.C. on Aegean peninsula.

2 Greeks expand 8th–6th century B.C., cover much of north mediterranean
coast. Interact with already old cultures: Egyptians and Babylonians.

3 Greek civ. peaked in 4th and 5th centuries B.C., capitol in Athens.

B Early Greek Math

1 Greeks first to do abstract math, methodically with proofs , all geometric.

2 Earliest greek math done in colonies, where interaction w/ remaining Bably.
and Egypt.

3 Pythagorean School/commune—studied properties of numbers , like triangular
and square numbers , “mystic” properties, and irrationality [Sec. 3.2]

4 Proofs of Pythagorean theorem and Irrationality of . [Sec 3.3]

III Hellenistic Age: Same Greek style, but location shift to Alexandria, Egypt (300s–100s
B.C.) [Chp. 4]

A History

1 In 300s B.C., Alexander the Great (of Macedonia) conquers Greek civ. and
rest of known world, but adopts and spreads greek culture through rest of
area. Center of intellectual activity shifts to his capitol in Egypt, Alexandria.
Begins “Hellenistic” (Greek-like) age.

2 Hellenistic life in Alexandria peaks 300 B.C. -100s B.C., then deteriorates
post 100 B.C., though a few persist sporadically til 400s A.D. (We skipped
most of chp. 5, “twilight of greek math” detailing this final period.)

3 First round of post-100s B.C. deterioration due to random political instability
in Egypt. E.g. an insecure leader banishes many disloyal scientists in
146 B.C.

B Alexandrian Math

1 Euclid (300s B.C.) and the Elements: book organizing all known greek math,
postulates (axioms), definitions, and propositions with proofs. [Sec 4.1, 4.2]

2 Euclid’s number theory: studying primes and divisibility, proving infinitely
many primes [Sec. 4.3]

3 Archimedes (200s B.C.), an engineering and creative genius. Made sequence
to approximate π well, and gave a clever proof of a relation between volumes
of sphere and circumscribed cylinder. Both methods were suggestive
of calculus (adding up infinitely many things of size zero ).

4 Eratosthenes (200s B.C.) some number theory, and gave a surprisingly accurate
measurement of circumference of earth

5 Ptolemy (100s A.D.) explained model of universe, with circular orbits about
earth, and earth off-center, to account for varying size of sun during day, in
an influential treatise on astronomy. Model lasted 14 centuries.

6 Scattered mathematics (that we skipped) through 400s A.D., though mostly
in decline. (see Chp. 5).

IV Romans (200s B.C. –400s A.D.) [Sec. 5.1, 5.4]

A Romans rise to power

1 Romans, based in Italy, grow in power til 200s-100s B.C., when conquer
Greece, proper (i.e. the Aegean peninsula).

2 Romans win Mesopotamia and Egypt (so Alexandria) in 1st century B.C.

3 Eventually, Romans conquer western part of middle east

B Romans don’t do math

1 Romans very practical: concentrate on feats of engineering

2 In Roman Empire, christianity sparked “antirationalism” movement, scorned
math and reasoning

C Alexandrians, under Roman rule , still do some math (chp. 5, we skipped)

1 Romans bring period of stability in Alexandria through 200s A.D. (“Pax
Romana”), Alexandrians do some math

2 As Roman Empire begins to lose stability (300s A.D.), math in Alex. trails
off, though still a few bright spots through the end.

D Fall of Rome: Alexandrian Legacy → Byzantine Empire (0 A.D. to 1400s A.D.)

1 Unrest (civil wars, no strong emporer) near end of Roman Empire, in 300s
A.D. leads to division between eastern and western empire, and establishment
of a parallel capitol in Constantinople.

2 Western Roman Empire falls to German barbarians in 400s A.D.

3 Region of empire near Constantinople does not fall when Western Roman
Empire does, but remains independent, called Byzantine Empire.

4 Some Alexandrian scholars drawn to Constantinople by unrest in Egypt
during the fall of Rome.

5 Alexandrian math preserved , but not expanded, in Constantinople, through
dark ages.

6 Constantinople falls 1453 to (uncivilized) Turks. Scholars flee to Italy, contribute
to renaissance (see later part of outline).