QUALIFYING EXAMINATION

Harvard University
Department of Mathematics
Tuesday 20 September 2005 (Day 1)

1. Let X be the CW complex constructed as follows. Start with Y = S¹, realized
as the unit circle in C ; attach one copy of the closed disc D = {z ∈ C : |z| ≤ 1}
to Y via the map ∂D → S¹ given by e^iθ 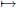e^4iθ ; and then attach another copy
of the closed disc D to Y via the map @D → S¹ given by e^iθ 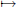e^6iθ .

(a) Calculate the homology groups H _*(X,Z).
(b) Calculate the homology groups H_*(X,Z/2Z).
(c) Calculate the homology groups H_*(X,Z/3Z).

2. Show that if a curve in R ³ lies on a sphere and has constant curvature then
it is a circle.

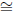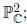3. Let X P⁵ be the space of conic curves in that is, the space of nonzero
homogeneous quadratic polynomials F ∈ C[A,B,C] up to scalars. Let Y ⊂ X
be the set of quadratic polynomials that factor as the product of two linear
polynomials; and let Z ⊂ X be the set of quadratic polynomials that are
squares of linear polynomials.

(a) Show that Y is a closed subvariety of X 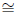P⁵, and find its dimension
and degree.
(b) Show that Z is a closed subvariety of X 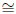P⁵, and find its dimension
and degree.

4. We say that a linear functional F on C([0, 1]) is positive if F (f) ≥ 0 for all
non- negative functions f. Show that a positive F is continuous with the norm
||F|| = F(1), where 1 means the constant function 1 on [0, 1].

5. Let D₈ denote the dihedral group with 8 elements.
(a) Calculate the character table of D₈.
(b) Let V denote the four dimensional representation of D₈ corresponding
to the natural action of the dihedral group on the vertices of a square.
Decompose Sym²V as a sum of irreducible representations.

6. Let f be a holomorphic function on C with no zeros. Does there always exist
a holomorphic function g on C such that exp(g) = f?

QUALIFYING EXAMINATION
Harvard University
Department of Mathematics
Wednesday 21 September 2005 (Day 2)

1. Let n be a positive integer. Using Cauchy’s Integral Formula , calculate the
integral

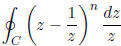
where C is the unit circle in C. Use this to determine the value of the integral

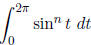
2. Let 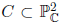be a smooth plane curve of degree d > 1. Let 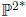be the dual
projective plane, and C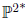^* ⊂ the set of tangent lines to C.

(a) Show that C^* is a closed subvariety of .
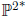(b) Find the degree of C^*.
(c) Show that not every tangent line to C is bitangent, i.e., that a general
tangent line to C is tangent at only one point. (Note: this is false if C is
replaced by a field of characteristic p > 0!)

3. Find all surfaces of revolution S ⊂ R³ such that the mean curvature of S
vanishes identically.

4. Find all solutions to the equation y" (t) + y(t) = (t + 1) in the space D'(R)
of distributions on R . Here δ(t) is the Dirac delta-function.

5. Calculate the Galois group of the splitting field of x⁵ − 2 over Q, and draw
the lattice of subfields.

6. A covering space f : X → Y with X and Y connected is called normal if for
any pair of points p, q ∈ X with f(p) = f(q) there exists a deck transformation
(that is, an automorphism g : X → X such that g ◦ f = f) carrying p to q.

(a) Show that a covering space f : X → Y is normal if and only if for any
p ∈ X the image of the map f_* : π₁(X, p) → π₁(Y, f(p)) is a normal
subgroup of π₁(Y, f(p)).
(b) Let Y 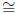S¹ ∨ S¹ be a figure 8, that is, the one point join of two circles.Draw a normal 3-sheeted covering space of Y , and a non-normal three-
sheeted covering space of Y .

QUALIFYING EXAMINATION
Harvard University
Department of Mathematics
Thursday 22 September 2005 (Day 3)

1. Let f : CP^m → CPⁿ be any continuous map between complex projective
spaces of dimensions m and n.

(a) If m > n, show that the induced map 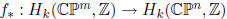is
zero for all k > 0.
(b) If m = n, the induced map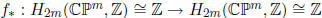
is multiplication by some integer d, called the degree of the map f. What
integers d occur as degrees of continuous maps f : CP^m → CP^m? Justify
your answer.

2. Let a₁, a₂, . . ., a_n be complex numbers. Prove there exists a real x ∈ [0, 1]
such that

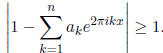
3. Suppose that ∇ is a connection on a Riemannian manifold M. Define the
torsion tensor via

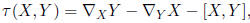
where X, Y are vector fields on M. ∇ is called symmetric if the torsion tensor
vanishes. Show that ∇ is symmetric if and only if the Christoffel symbols with
respect to any coordinate frame are symmetric, i.e. 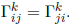Remember that
if {E_i} is a coordinate frame, and ∇ is a connection, the Christoffel symbols
are defined via

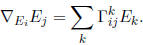
4. Recall that a commutative ring is called Artinian if every strictly descending
chain of ideals is finite. Let A be a commutative Artinian ring.
(a) Show that any quotient of A is Artinian.
(b) Show that any prime ideal in A is maximal.
(c) Show that A has only finitely many prime ideals.

5. Let X ∈ Pⁿ be a smooth hypersurface of degree d > 1, and let A P^k ∈ X a
k-dimensional linear subspace of Pⁿ contained in X. Show that k ≤ (n−1)/2.

6. Let 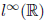denote the space of bounded real sequences {x_n}, n = 1, 2, . . . .
Show that there exists a continuous linear functional 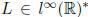with the
following properties:

a) inf x_n ≤ L({x_n}) ≤ sup x_n,
b) If 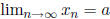then L({x_n}) = a,
c) L({x_n}) = L({x_n+1}).
Hint: Consider subspace 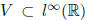generated by sequences {x_n+1 − x_n}.
Show that and apply Hahn-Banach.