Matrix Algebra Review
Definition. An m*n matrix, Am*n, is a rectangular array of real
numbers with m rows and n
columns. Element in the ith row and the jth column is denoted by aij .
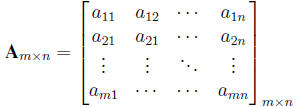
Definition. A vector a of length n is an n*1 matrix with each element
denoted by ai. The ith
element is called the ith component of the vector and n is the
dimensionality.
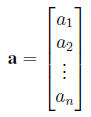
1. Two matrices A and B of the same dimensions can be added . The sum A + B
has (i, j) entry
aij + bij . So
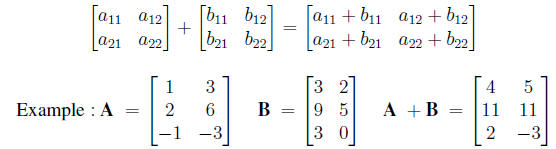
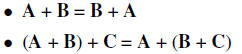
2. A matrix may also be multiplied by a constant c. The product cA is the
matrix that results
from multiplying each element of A by c. Thus
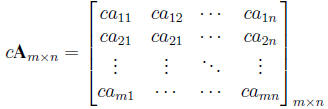
3. The transpose operation A T or A' of a matrix changes the columns into rows
so that the first
column of A becomes the first row of AT , the second column becomes second row,
and etc.
So the (i,j)th element in Am*n becomes the (j,i)th
in the transpose
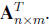
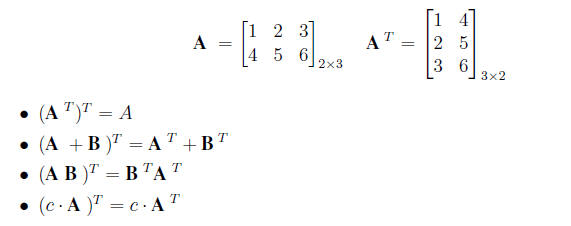
4. We can define matrix multiplication A B if the number of elements in a row
of A is the same
as the number of elements in the columns of B. E.g. when A is (p*k) and B is
(k*n). An
element of the new matrix AB is formed by taking the inner product of each row
of A with
each column of B. The matrix product AB is

Special Square Matrix
1. A square matrix A is said to be symmetric if A = AT or aij= aji for all i and j.
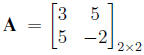
is symmetric,
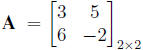
is not symmetric
2. Diagonal Matrix.
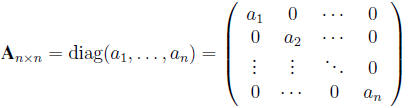
3. Identity Matrix.
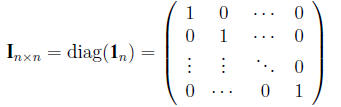
The identity matrix is a square matrix with ones on the diagonal and zeros
elsewhere . It
follows from the definition of matrix multiplication that the (i, j) enrty of AI
is
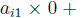
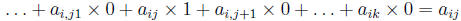 .
So AI = A . Similarly, IA = A .
.
So AI = A . Similarly, IA = A .
Therefore matrix I acts like 1 in ordinary multiplication.
The fundamental scalar relation about the existence of an inverse number a-1
such that
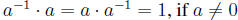 , has the following matrix algebra extension .
, has the following matrix algebra extension .
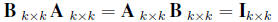
then B is called the inverse of A and is denoted by A-1.
Other Matrix Properties
1. Trace. The sum of the diagonal elements,
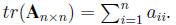
2. A square matrix that does not have a matrix inverse is called a singular
matrix
The inverse of a 2*2 matrix is given by
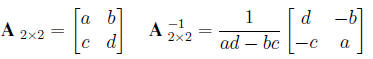
3. A matrix is singular if and only if its determinant is 0. The determinant
of a matrix A is
denoted as |A| The determinant of a 2*2 matrix is given by
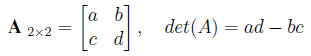
Examples 1. Simultaneous equations
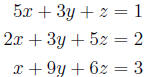
We can rewrite the above three equations as a single matrix equation.
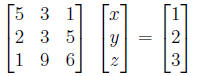
Example 2. Variance/Covariance Matrix
For a vector of random variables,
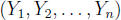 ,
we can write a matrix containing their variances
,
we can write a matrix containing their variances
and their covariances. Let
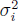 be the variance of Yi and let covij be the covariance between Yi and
be the variance of Yi and let covij be the covariance between Yi and
Yj , i < j. Then the variance/covariance matrix for
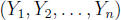 is
is
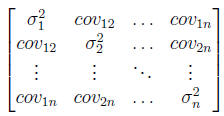
Also note that the above can be written as
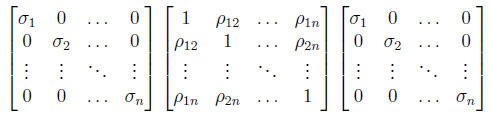
where 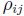 is the
correlation of Yi and Yj . Note that all of these matrices
are symmetric. Furthermore,
is the
correlation of Yi and Yj . Note that all of these matrices
are symmetric. Furthermore,
the terms on the diagonal of the variance/covariance matrix must be positive and
terms off
the diagonal of the correlation matrix are bounded by -1 and 1.
Example 3. Multiple Linear Regression
We have a response Y and a set of p independnet variables
X 1,X2, . . . ,Xp. Assume we have n
observations and for each i = 1, . . . , n observation, we assume
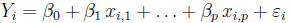
where 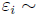 Normal (0,
Normal (0,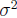 ).
).
We can represent n observations simultaneously in matrix form as
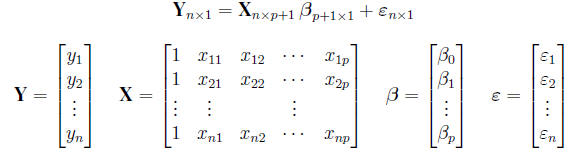
The residual 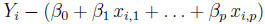 can be
written as
can be
written as
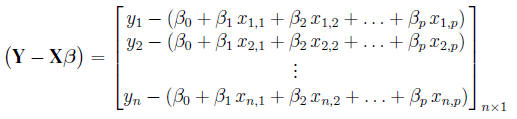
The residual sum of squares (RSS) is
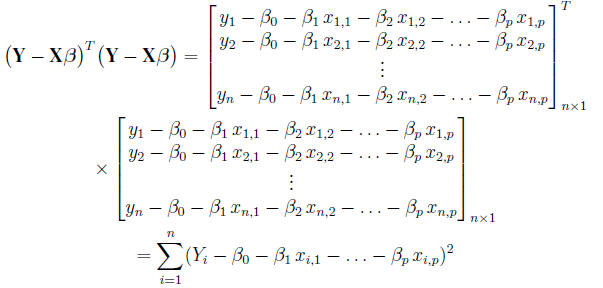
Minimizing the above RSS gives the usual least -squared estimate for β
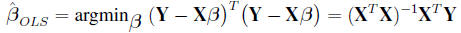
| Prev | Next |