RANGE OF FUNCTIONS

A relation is a function if and only if there is exactly one output for every input. A function has an independent
variable x , and a dependent variable y.

The range of a function refers to all of the possible values for the dependent variable y that a function can have.

I. When a function is represented as a set of ordered pairs, the first coordinate is the input and the second
coordinate is the output . The output values refer to the range.

Example: (1, 3) (4, 6) (5, 7) (7, 9) (9, 11)

In this case the range would be {3, 6, 7, 9, 11}

Range is denoted by f (x) when a function is given the name “f”.

II. When a function is represented or given as an equation, the range can be found graphically or by using the
function’s inverse. (For more information about inverses refer to the Function and Inverse Functions Handout.)

Finding the Range Graphically:
Depending on the type of function, the functions graph and range varies.

The range of functions is subject to change depending on whether the function has vertical shifts or is reflected,
flipped, about the x-axis.

* The linear , cubic, logarithmic, and cube root functions are the exceptions. The range for these functions is all
real numbers , written as (−∞,∞) or {y | y ε }. *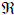

The following functions have a set range and are in their standard state.

Linear Function Range: (− ∞,∞) or {y | y ε 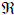}	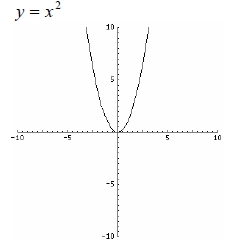Quadratic Function Range: [0,∞) or {y | y ≥ 0}		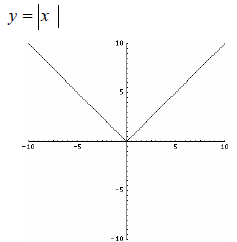Absolute Value Function Range: [0,∞) or {y | y ≥ 0}
Square Root Function Range: [0,∞) or {y | y ≥ 0}	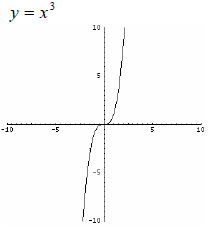Cubic Function Range: (− ∞,∞) or {y | y ε 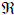}		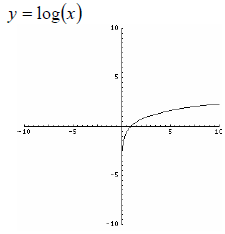Logarithmic Function Range: (− ∞,∞) or {y | y ε }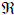
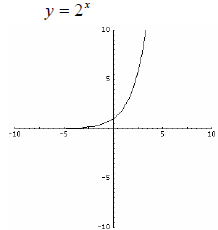Exponential Function Range: [0,∞) or {y | y ≥ 0}		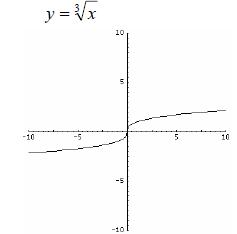Cube Root Function Range: (− ∞,∞) or {y | y ε }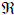

The standard state function is represented as f (x) so when a number is added or subtracted from f (x), y = f (x) ±
k where k is a number then a vertical shift occurs. For example, the standard state function f (x) = x³ experiences
a vertical shift when f (x) = x³ + 5 or f (x) = x³ - 1.

Also, when a negative sign is placed before the standard state function, y = - f (x), then the graph of the function
is reflected about the x-axis.

The following functions have changed by a vertical shift or were flipped about the x-axis, and therefore
their range has been changed.

Here the standard state function, f (x) = | x | has experienced a vertical shift and the function has been reflected about the x-axis. Therefore the range of the function changes to Range: [2,−∞) or {y | y ≤ 2}

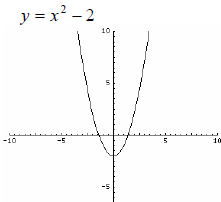The standard state function, f (x) = x² has experienced a vertical shift. Therefore the range of the function changes to: Range: [− 2,∞) or {y | y ≥ 2}

For rational functions the range depends on the function’s horizontal asymptotes or slant asymptotes which
break up the range into two intervals .

Rational functions are composed of two polynomials being divided .

In this example, there is not a slant asymptote but there is a horizontal asymptote.

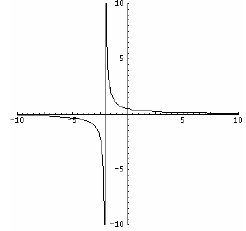
Example: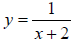 Horizontal asymptote: y = 0 Range: (− ∞,0),(0,∞) or {y | y ≠ 0} The asymptote excludes the value x=0 and breaks up the graph as shown.

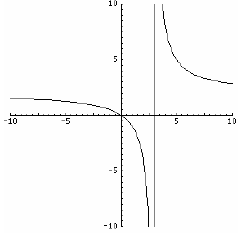
Example: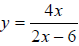 Horizontal asymptote: y = 2 Range: (− ∞,2),(2,∞) or {y | y ≠ 2} The asymptote excludes the value x=3 and breaks up the graph as shown.

The range can also be found by taking the inverse of the function, written f ^-1 (x), given and finding the domain
of the inverse.

To find the inverse of a function you will interchange the independent and dependant variables and then solve
for the dependent variable.

Example:	y = x² + 6
Interchange the x and y variables:	x = y² + 6
Next, solve for y :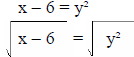

The resulting equation is the inverse :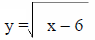

Find the domain of the inverse: Domain: (0.∞) or {y | y ≥ 0}

Therefore the range of the original function, y = x² + 6, is: (0.∞) or {y | y ≥ 0}

(If the function does not have an inverse, for example f (x) = | x | does not have an inverse, use the other methods

listed above to find the range.)