Simplifying Fractions
Writing a Number as a Product of Prime Factors
A prime number is a whole number greater than 1 that cannot be evenly
divided except by itself and 1. If you examine all the whole numbers from 1 to
50, you will find 15 prime numbers.
The First 15 Prime Numbers
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47
Composite Number
A composite number is a whole number greater than 1 that can be divided by
whole numbers other than 1 and itself.
Divisibility Tests
1. A number is divisible by 2 if the last digit is 0, 2, 4, 6, or 8.
2. A number is divisible by 3 if the sum of the digits is divisible by 3.
3. A number is divisible by 5 if the last digit is 0 or 5.
Writing Numbers as Products of Prime Factors
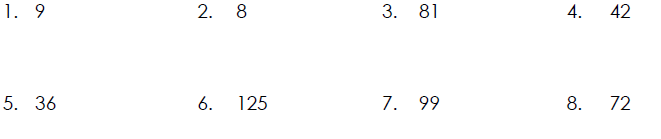
Determining If a Number is Prime
Determine which of these whole numbers are prime. If a number is composite,
write it as the product of prime factors.
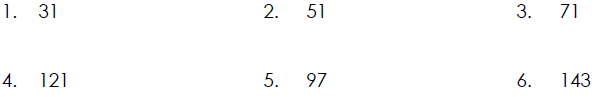
Reducing a Fraction to Lowest Terms
A fraction is called simplified , reduced, or in lowest terms if the numerator
and
denominator have only 1 as a common factor .
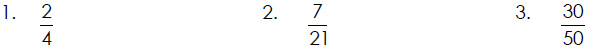
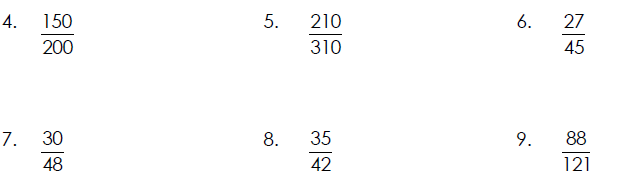
Equality Test for Fractions
After we simplify, how can we check that a reduced fraction is equivalent to the
original fraction? If two fractions are equal, their diagonal products or cross
products are equal. This is called the equality test for fractions. Equivalent
fractions are two fractions that are equal. For any two fractions where a, b, c,
and d are whole numbers and b ≠ 0, d ≠ 0, if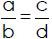 then
a×d=b×c.
then
a×d=b×c.
Determining Whether Two Fractions are Equal
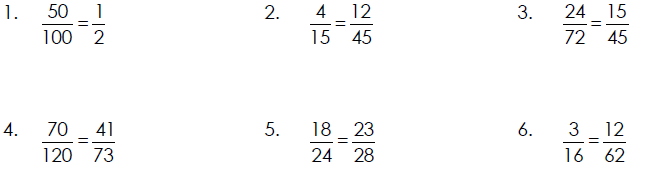
Real -World Applications
1. Medical students frequently work long hours. Susan worked a 16-hour shift,
spending 12 hours in the emergency room and 4 hours in surgery. What
fractional part of her shift was she in the emergency room? What fraction
part of her shift was she in surgery?
2. William works for a wireless communications company
that makes beepers
and mobile phones. He inspected 315 beepers and found that 20 were
defective. What fractional part of the beepers were not defective?
2.2 Homework
Pages 124–127 #1, 3, 5, 11, 17, 21, 27, 35, 41, 47, 51, 59, 63, 69, 77, 81, 89
2.3 – Converting Between Improper Fractions and Mixed
Numbers
Vocabulary
• Proper Fraction - A fraction in which the numerator is less than the
denominator. The fractions 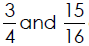 are proper
fractions.
are proper
fractions.
• Improper Fraction - A fraction in which the numerator is greater than or equal
to the denominator. The fractions 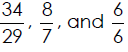 are all
improper fractions.
are all
improper fractions.
• Mixed Number - A number created by the sum of a whole number greater
than 1 and a proper fraction. The numbers 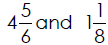 are
both mixed
are
both mixed
numbers. Mixed numbers are sometimes referred to as mixed fractions.
Changing a Mixed Number to an Improper Fraction
1. Multiply the whole number by the denominator of the fraction.
2. Add the numerator of the fraction to the product found in step 1.
3. Write the sum found in step 2 over the denominator of the fraction.
Examples of Changing Mixed Numbers to Improper Fractions
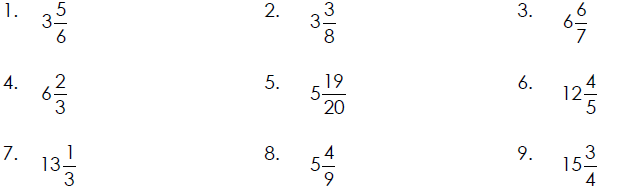
Changing an Improper Fraction to a Mixed Number
1. Divide the numerator by the denominator.
2. Write the quotient followed by the fraction with the remainder over the
denominator.
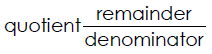
Examples of Changing Improper Fractions to Mixed Numbers
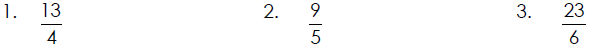
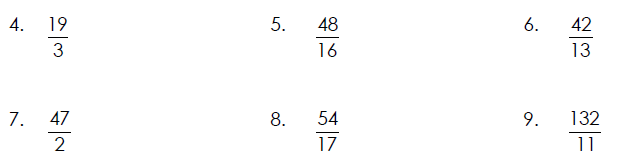
Reduce Each Mixed Number
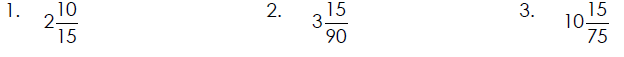
Reduce Each Improper Fraction
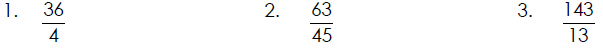
Change to a Mixed Number and Reduce
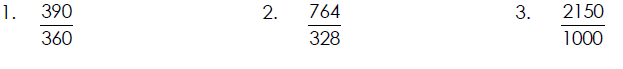
Applications
1. For the Northwestern University alumni homecoming, the students studying
sculpture have made a giant replica of the school using
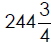 pounds of
pounds of
clay. Change this number to an improper fraction.
2. To paint the walls of the new gymnasium, the custodian
took measurements.
Based on his calculations , he determined he needed
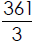 gallons of paint.
gallons of paint.
Write this as a mixed number.
2.3 Homework
Pages 132–134 #1, 7, 13, 23, 27, 37, 41, 43, 47, 63, 77, 85
2.4 – Multiplying Fractions and Mixed Numbers
Multiplying Two Fractions That Are Proper or Improper
In general, for all positive whole numbers, a, b, c, and d,

Multiplying a Whole Number by a Fraction
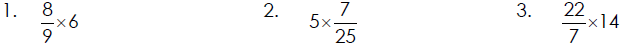
Multiplying Mixed Numbers
Change any mixed number to an improper fraction before multiplying.
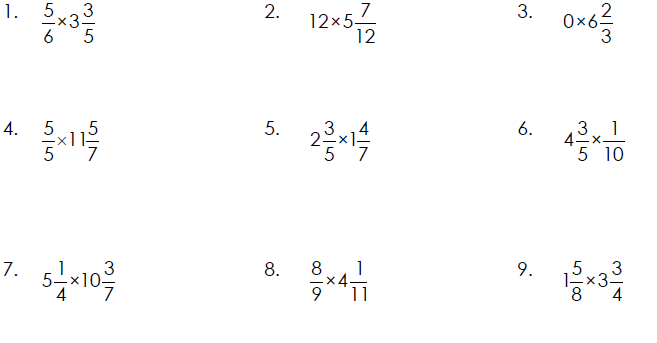
Applications
1. An area in the Midwest is a designated tornado danger zone. The land is
 miles long and
miles long and
 miles wide. Find the area of the tornado
danger
miles wide. Find the area of the tornado
danger
zone. (Hint: The area of a rectangle is the product of the length times the
width.)
2. A jeep has  gallons
of gas. The jeep averages 12 miles per gallon. How
gallons
of gas. The jeep averages 12 miles per gallon. How
far will the jeep be able to go on what is in the tank?
3. The dormitory rooms in Selkirk Hall are being carpeted.
Each room requires
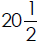 square feet of carpet. If there are 30
rooms, how much carpet is
square feet of carpet. If there are 30
rooms, how much carpet is
needed?
4. Russ purchased a new Buick LeSabre for $26,500. After
one year the car was
worth 4/5 of the purchase price. What was the car worth after one year?
5. There were 1340 students are the Beverly campus of
North Shore Community
College during the spring 2006 semester. The registrar discovered that 2/5 of
these students live in the city of Beverly. He further discovered that 1/4 of
the
students living in Beverly only attend classes on Monday, Wednesday and
Friday. How many students at the Beverly campus live in the city of Beverly
and attend classes only on Monday, Wednesday, and Friday?
2.4 Homework
Pages 139–141 #1, 13, 23, 29, 33, 41, 49, 53, 59, 61
| Prev | Next |