Solving Equations

D.

1. Write 4x • 5y • 3x • x in exponential form .

2. Translate the following into an equation :
Three times the difference of a number x and 7 is 6

3. Find the sum of the matrices :

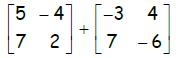
4. Find the difference of the matrices:

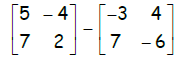
5. Graph the inequality :

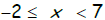
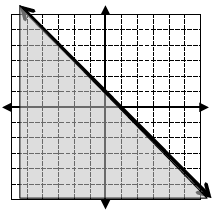
6. Write the inequality for the half -planed graph:

7. Simplify : (-3x²y³)(5xy³)

8. Simplify: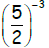

9. Simplify: (-2x³y²)(3xy³)²

Use the quadratic formula to solve each equation:

10. x² + 4x = 5

11. 3x² – 4x - 2 = 0

12. 6x² + x – 2 = 0

13. x² + 6x + 4 = 0

E.
Name the opposite and reciprocal of each:

1. 3
2. -7
3. 4/5
4. -6/7

Evaluate for x = 2 and x = -2

5. 2x² – x
6. -3x²
7. - x²
8. ½x -2
9. (-x) ²

Evaluate for x = 7 and y = -3

10. (x + y)²
11. x² + y²
12. (x - y)²
13. x² - y²

Write algebraic expressions for each .

14. The difference between a and m ____________________
15. Seven less than a number, y ____________________
16. Eight more than five times a number c ____________________
17. Twice the sum of a number, x, and nine ____________________

Graph the following equations.

18. y = 2x – 1

19. y = -2

20. x = 3

21. 2x – 4y = 8

22. y = -2/3x + 2

F.
Write the equation of each line.

1. Slope = 3, passing through (1, 2)
2. m = -1, passing through (1, 2)
3. m = 4, passing through (-2, 3)

Perform the indicated operations and simplify .

Factor completely .

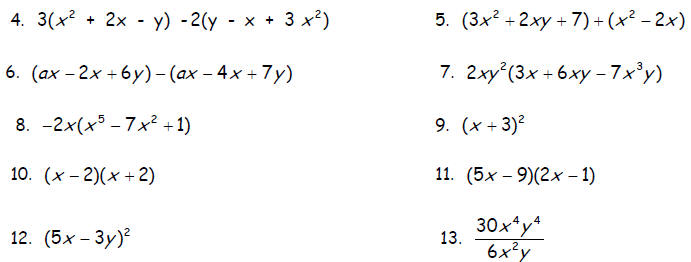
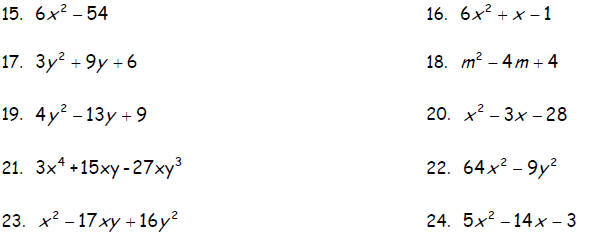
G.
Solve each of the systems of linear equations.
1. –4x + 2y = 2
 4x + 3y = -12

2. x – 2y = 16
x + y = 10

3. 3x + 2y = 11
x = 3y

4. 3x – 5y = 63
2x + 3y = -15

Rewrite in the following in decimal form .

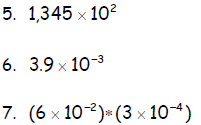
Rewrite the following in scientific notation form.

8. 2450
9. 0.000372
10. 1.78
11. 47.2

Simplify.

H.
Simplify and leave in radical form.

Identify whether the parabola opens up or down and find the vertex.

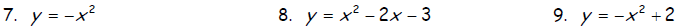
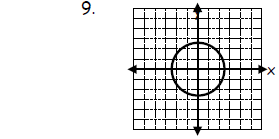
Graph.

Determine whether the information defines a function.

11. {(3, 4), (5, 4), (7, 3), (2, 8)}

12.

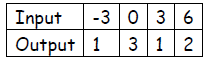
Identify the domain and range of the function.

13. {(2, 4), (5, 4), (7, 3), (9, 8)} Domain: _____________ Range: _____________

Evaluate the function.

14.

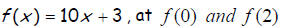
I.
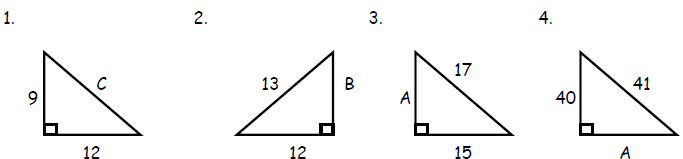
Use the Pythagorean Theorem to find the missing length of a right triangle.

Use the distance formula to find the distance between the two points.

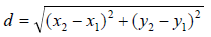
6. (6, 9) and (14, 24)
7. (-5, 8) and (2, -16)
8. (-3, -5) and (-11, 5)
9. (5, 6) and (7, -10)

Find one of the many proofs of the Pythagorean Theorem. Write the solution , draw the solution and explain it in your own words.