Transformations of Functions
PART A: Vertical Shifts
| Graph A | Graph B |
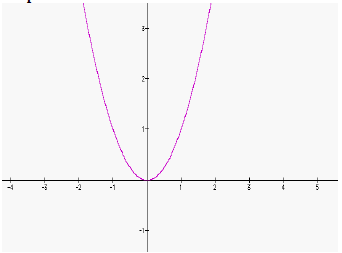 |
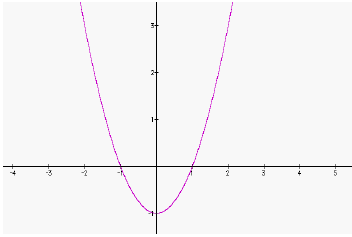 |
Notice that Graph B has been shifted vertically downward by one unit.
1. The equation for Graph A is: f(x) = __________
2. The equation for Graph B is: g(x) = __________
3. Now write a formula that relates f(x) and g(x) in a single equation:
__________________________
Looking for Vertical Shifts in a Table of Data
Table A
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| f(x) | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
Table B
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| g(x) | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
4. Compare outputs for corresponding inputs for the f and g functions. What do you notice?
5. Using function notation such as f(x)= _______, write a formula for the function in Table A.
6. Using function notation such as g(x) = _______, write a formula for the function in Table B.
7. Now write a formula that relates f(x) and g(x) in a single equation: __________________________
8. Does this transformation primarily affect input or output values ?
PART B: Horizontal Shifts
| Graph A | Graph B |
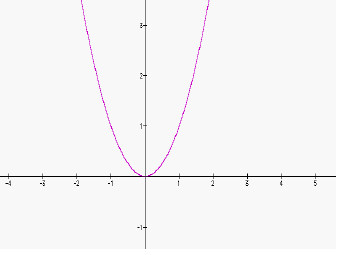 |
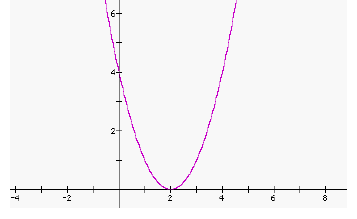 |
Notice that Graph B has been shifted horizontally to the right by two units .
1. The equation for Graph A is: f(x)= __________
2. The equation for Graph B is: g(x) = __________
3. Now write a formula that relates f(x) and g(x) in a single equation:
_____________________________
Looking for Horizontal Shifts in a Table of Data
Table A
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| f(x) | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 25 |
Table B
| x | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| g(x) | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 25 |
4. Compare inputs for corresponding outputs for the f and g functions. What do you notice?
5. Using function notation such as f(x)= _______, write a formula for the
function in Table A.
6. Using function notation such as g(x) = _______, write a formula for the
function in Table B.
7. Now write a formula that relates f(x)and g(x) in a single equation:
_________________________
8. Does this transformation primarily affect input or output values?
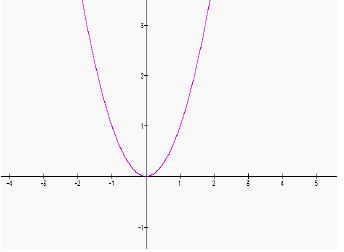
PART C: Reflection Across an Axis
| Graph A | Graph B |
 |
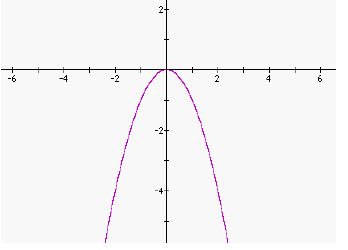 |
1. Graph A and Graph B are reflections of each other across which axis?
_______________
2. Use the graphs above to fill in the y-values:
| Graph A | Graph B |
 |
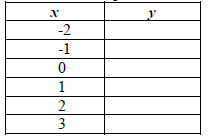 |
3. What pattern do you observe when you compare the 2 columns of y-values?
When you reflect a graph across
the x-axis, what happens to the y- coordinate values ? Explain.
4. The equation for Graph A is: f(x) = __________
5. The equation for Graph B is: g(x) = __________
6. When the graph of y = f(x) is reflected across the x-axis, how does the
equation change?
7. Does this transformation primarily affect input or output values?
| Graph C | Graph D |
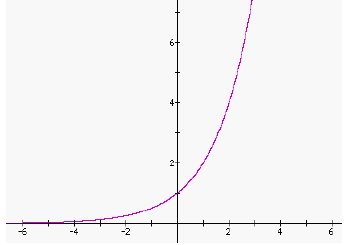 |
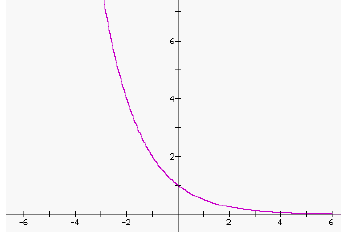 |
8. Graph C and Graph D are reflections of each other across which axis? _______________
9. Fill in the missing x-values:
| Graph C | Graph D |
 |
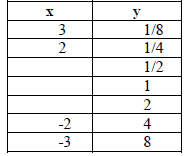 |
10. What pattern do you observe when you compare the 2 columns of x-values?
When you reflect a graph across
the y-axis, what happens to the x-coordinate values? Explain.
11. The equation for Graph C is: f(x) = __________
12. The equation for Graph D is: g(x) = __________
13. When the graph of y = f(x) is reflected across the y-axis, how does the
equation change?
14. Does this transformation primarily affect input or output values?
PART D: Odd and Even Functions
1. On each set of axes, draw a graph that is symmetric about the y-axis.
2. On each set of axes, draw a graph that is symmetric about the origin.
3. A function that is symmetric about the y-axis is called an EVEN
function. A function that is symmetric
about the origin is called an ODD function.
Determine whether each of the functions is EVEN, ODD or NEITHER by graphing on
your calculator
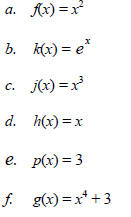
PART E: Overview
1. Given 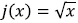
a. Give the formula for the function that transforms j(x) by shifting its graph down 4.
b. Give the formula for the function that transforms j(x) by shifting its graph to the right 5.
c. Give the formula for the function that transforms j(x) by reflecting it over the y-axis.
d. Give the formula for the function that transforms j(x) by shifting its graph up 6 and left 2.
e. Give the formula for the function that transforms j(x) by shifting its graph down 7 and reflects over the x-axis.
Practice Problems
Pg 201 #20-25,27
Pg 209: #3,5,6,7,25
MAT 150: Sections 5.3-5.4 More Transformations of Functions
PART A: Vertical Stretches and Compressions
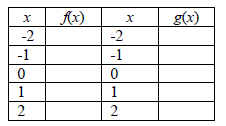
| 1. Complete the table for f(x)=x^2 and g(x)=2x^2 | 2. Complete the table for f(x)=x^2 and g(x)=0.5x^2 |
 |
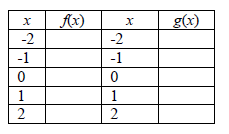 |
| 3. Using the points from the table, graph f(x)=x^2 and g(x)=2x^2 | 4. Using the points from the table,graph f(x)=x^2 and g(x)=0.5x^2 |
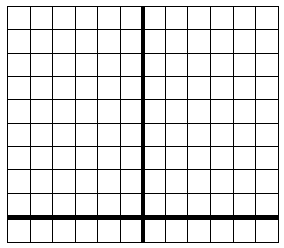 |
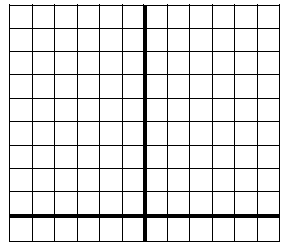 |
5. Describe how function g is a transformation of function f in #1. Write the transformation using function notation.
6. Describe how function g is a transformation of function f in #2. Write the transformation using function notation.
7. Does this transformation primarily affect input or output values?
PART B: Horizontal Stretches and Compressions
| 1. Complete the table for f(x)=x^2 and g(x)=2x^2 | 2. Complete the table for f(x)=x^2 and g(x)=0.5x^2 |
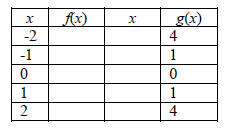 |
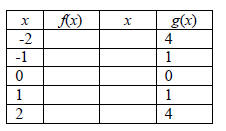 |
| 3. Using the points from the table, graph f(x)=x^2 and g(x)=2x^2 | 4. Using the points from the table,graph f(x)=x^2 and g(x)=0.5x^2 |
 |
 |
5. Describe how function g is a transformation of function f in #1. Write the transformation using function notation.
6. Describe how function g is a transformation of function f in #2. Write the transformation using function notation.
7. Does this transformation primarily affect input or output values?
PART C: Transformations Recap
Describe how the function g has been changed from the function f. In your description, use phrases such as:
“reflection through the _____ - axis”
“vertical shift up (down) by ______ units”
“horizontal shift to the right (left) by ________ units”
“vertical stretch/compression by a factor of ______”
“horizontal stretch/compression by a factor of _______”

11. Given the graph of the function f(x) shown below. Graph each of the given transformations
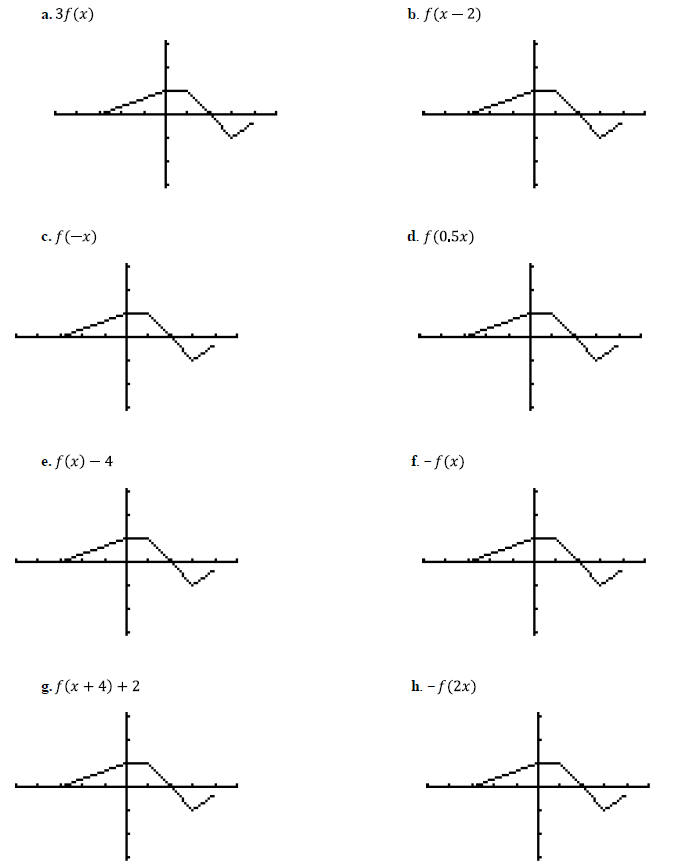
Practice Problems:
Pg 216: 8,10,28
Pg 223: 3,5,19
MAT 150: Sections 5.5 The Family of Quadratic Functions
PART A: The Different Forms of the Quadratic Function
Like many of the functions you study, quadratic function
can be written in more than one format. Strive to be
flexible in moving from one format to another depending on what information you
need.
Standard Form
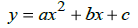
This form conveys the following information or allows you to quickly determine:
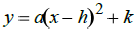
This form conveys the following information or allows you to quickly determine:
Factored Form
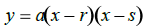
This form conveys the following information or allows you to quickly determine:
PART B: Using the Different Forms : (use your calculator to check your answer)
| 1. Determine the zeros of the function : | 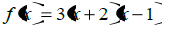 |
| 2. Determine the vertex of the graph of: Is the vertex a maximum or a minimum? |
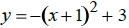 |
| 3. Determine the y- intercept of the
graph of: Is the parabola concave up or concave down? |
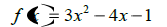 |
| 4. Write an equation for the line of symmetry for
the graph of Describe the transformations of x^2 that this equation represents |
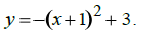 |
| 5. Determine the concavity and the zeros of: | 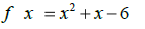 |
| 6. Is the graph of f concave up or concave down? What is the y-intercept of the graph? |
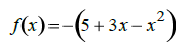 |
| 7. Describe the characteristics of the function and its graph in as much detail as you can: | 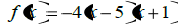 |
PART C: Writing Equations for Quadratic Functions
1. Write a quadratic equation for a function with zeros x = 3 and x = -1. What is the y-intercept of the graph of this function?
2. Write a quadratic equation for a function with zeros x
= 3 and x = -1 and a y-intercept of (0, 6).
3. Write a quadratic equation for a function with zeros x = -6 and x = 2 and a y-intercept of (0, 5).
4. Write the equation of a quadratic function whose graph has a vertex at (4, 2) and a y-intercept of (0, 6).
5. Write the equation of a quadratic function whose graph has a vertex at (4, 2) and a y-intercept of (0, -4).
6. Write the equation of a quadratic function whose graph has a vertex at (-7,-3) and contains the point (-3,-7).
| Prev | Next |