Comparing Fractions

1. Julie says that the picture in Figure 3.58 shows that ¼ > ½ by comparing the
areas . Explain carefully the error in Julie’s reasoning.

Julie is making the usual mistake of confusing the wholes. The whole she is using for the
fraction ¼ is bigger (in fact, more than twice as big) as the whole she pictures for the
fraction ½. It is true that—in her picture—the shaded area on the left is larger than the
one on the right, although even that fact isn’t entirely obvious.

To help Julie you can draw the wholes the same size. You can also put this into the
context of a story: On Tuesday, Julie and three other girls shared one brownie. On
Wednesday, Julie and two other girls shared a brownie of the same size. On which day
did Julie get a bigger piece?

Another way to help Julie remember to use the same wholes is to use counting numbers.
Clearly 2 yards is longer than 3 feet, but that doesn’t mean that 2 is bigger than 3.

2. In your own words, explain in detail why we can determine which of two fractions
is greater by giving the two fractions common denominators . What is the rationale
behind this method? What are we really doing when we give the fractions common
denominators?

If we have drawn pictures of the two fractions using the same size whole—say, a
rectangle divided into equal pieces for each fraction—then, if the denominators of the
two fractions are not the same, we have different sized pieces in the two pictures. By
giving the two fractions a common denominator , we are just making the pieces the same
size so that we can compare how many are in one picture, as opposed to how many are in
the other picture.

15. Sam has a method for comparing fractions: He just looks at the denominator.
Same says the fraction with the larger denominator is smaller because, if there are
more pieces, each piece is smaller. Discuss Sam’s idea.

Sam has probably come up with his method for comparing fractions by comparing unital
fractions, which are fractions with the number 1 in the numerator . Sam’s method does
work when comparing unital fractions. It is true that ¼ < ½, for example. However, when
either of the fractions to be compared are not unital fractions, Sam’s method may not
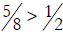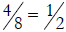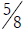work. For example,   because and   is more than .

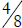17. Malcolm says that 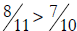  because 8 > 7 and 11 > 10. Even though it is true
that 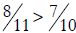, is Malcolm’s reasoning correct? If Malcolm’s reasoning is correct,
clearly explain why. If Malcolm’s reasoning is not correct, give Malcolm two
examples that show why not.

Malcolm’s reasoning happened to give the right answer in this case but reasoning is only
valid if you can depend on it to give right answers always. In general, it is incorrect to
argue this way. For instance, 3 > 1 and 7 > 2 but it is not true that 3/7 > 1/2 .
You can do the same thing with 8> 7 and 17 > 14 .

It is important not just to show children how to get the right answer but to help them
understand where their own thinking led them astray. In Malcolm’s case you could say
that you have two children; one gets 8/11 of a brownie and the other gets 7/10 of a
brownie. The first one got more pieces—that is true. But the first brownie was divided
into more pieces in the first place; so the first child got smaller pieces than the second
child. In general, if you get more pieces, but the pieces are smaller, you can’t really say
anything until you know more about the exact sizes involved.

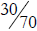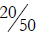18.a) Is it valid to compare and by canceling the 0s and comparing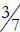
and 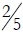instead? Explain your answer.
b) Is it valid to compare 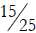and 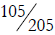by canceling the 5s and comparing
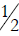
and 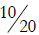instead? Explain your answer.
c) Write a paragraph discussing the distinction between your answer in (a) and your
answer in (b).

a. It is fine to compare in this fashion because 30/70 = (3 × 10) / (7 × 10) =
3/7 and also 20/50 = (2 × 10)/(5 × 10) = 2/5. In other words, you are comparing the
same numbers, just written differently.

b. On the other hand there is no sense in “canceling the fives” in 15/25, because 15/25
does not equal (1 × 5) / (2 × 5) .

Actually you can divide by 5, because 15 / 25 = (3 × 5) / (5 × 5) = 3/5.

c. The reason you can “cancel” the zeroes in a number like 30/70 is exactly because we
use a base of ten for our number system . A number written as the numeral 30 means
precisely 3 × 10 . It works with more digits, too, of course: 2350 = 235 × 10. There
is no other digit that this works for; 35 does not mean 3 × 5. It would be a very
different kind of enumeration scheme if it did!There are a few sporadic cases where you
can “cancel” like this:

Start with 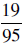; cancel the

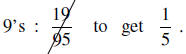
And, indeed, 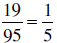. Can you think of any other two-digit numbers that work like
this?