Quadratic Functions
A quadratic function is a function of the form
where 
are constants, and
.
The graph of a quadratic function is called a
• When a > 0,
• When a < 0,
The turning point on the parabola is called the
The vertical line passing through the vertex is called the
Example. Graph the function using translation of y
= x2. Find
the vertex , axis of symmetry, and intercepts .
y = x2 − 6x + 8
The Graph of y = ax2 Let
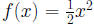g(x) = x2, h(x) = 2x2,
and j(x) = −2x2.
To summarize , y = ax2 is a parabola, similar to y = x2,
and
• If a < 0, then the graph opens
• If a > 0, then the graph opens
• If |a| > 1, then the graph opens
• If |a| < 1, then the graph opens
 |
|
 |
 |
 |
|
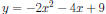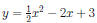Extreme Values
A quadratic function will have a
when
A quadratic function will have a
when
This will always happen at the
Find the maximum / minimum output for the following functions:
• f(x) = x2 − 4x + 3
• f(x) = −2x2 + 6x − 9
• f(x) = 4x2 + 8x + 3
The Vertex Form of a Quadratic Function
The equation of the parabola y = ax2+bx+c can always be rewritten
as
where the is
and the
is
Example. Find the quadratic function which passes
through the
point (−2, 3) and has a vertex of (1, 5).
Example. For what value of c will the minimum value
of f(x) =
x2 − 4x + c be -7?
Example. For what value of c will the maximum value
of f(x) =
x2 + 6x + c be 12?
| Prev | Next |