Get it on Google Play Get it on Apple Store

Using Microsoft Excel 2007 to Perform Matrix Operations

PURPOSE:
This handout was created to provide you with step-by-step instructions on how to perform various
matrix operations when using Microsoft Excel 2007.

Many of the Microsoft Excel functions that you will be using to complete these matrix operations are array
functions – returning more than one value at a time. To enter an array function into a Microsoft Excel
worksheet, you must hold down the CTRL and SHIFT keys while pressing the ENTER key:
CTRL+ SHIFT+ ENTER. Once this is done, braces will surround the array formula.

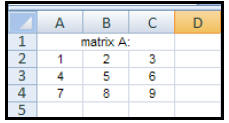
How to organize (enter) data in matrices:

A computer spreadsheet is a series of small blocks (cells) where the columns
are labeled with capital letters and the rows are labeled by numbers. To enter
a matrix into Microsoft Excel, simply type each matrix element into its own
small block (cell).

Pressing ENTER after each entry will usually make the cursor go down to the
next cell. (See the note below.) Pressing the RIGHT ARROW key after each
entry will make the cursor move to the next cell to the right.
NOTE: The default direction is down, but you can change the direction in which the cursor moves in through the EXCEL OPTIONS dialog box:
MICROSOFT OFFICE BUTTON EXCEL OPTIONS → ADVANCED → UNDER EDITING OPTIONS
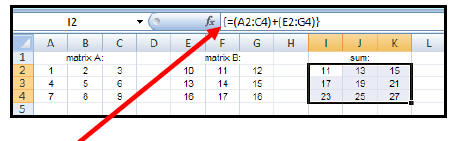
How to add matrices :

1. Enter the data of each matrix.

2. Highlight another section of the worksheet
(near the given matrices) that has the
same dimensions as the answer matrix.

Let's say that we wish to find: [A] + [B]
Since we are adding two 3 x 3 matrices ,
the sum matrix will also be 3 x 3.
 
3. Type: = (A2:C4)+(E2:G4) (This will appear in the formula bar.)


4. Since this answer will result in an array (matrix), you will need to: CTRL+ SHIFT+ ENTER
(NOTE: Braces will surround the formula .)

  
How to subtract matrices :

1. Enter the data of each matrix.

2. Highlight another section of the worksheet
(near the given matrices) that has the
same dimensions as the answer matrix.

Let's say that we wish to find: [A] – [B]
Since we are subtracting two 3 x 3 matrices, the difference matrix will also be 3 x 3.

3. Type: =(A2:C4)–(E2:G4) (This will appear in the formula bar.)

4. Since this answer will result in an array (matrix), you will need to: CTRL+ SHIFT+ ENTER		  
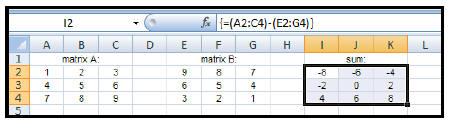How to find the transpose of a matrix:

1. Enter the elements of the given matrix.

2. Highlight another section of the worksheet (near the
given matrix) that has the same dimensions as the
answer matrix.

Since we are finding the transpose of a 2 x 3 matrix,
the answer will be a 3 x 2 matrix.

3. Type: = TRANSPOSE(A2:C3) (This will appear in the formula bar.)

4. Since this answer will result in an array (matrix), you will need to: CTRL+ SHIFT+ ENTER		  
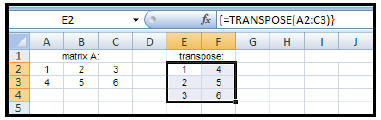How to multiply a matrix by a scalar ( real number ):

1. Enter the elements of the given matrix.

2. Highlight another section of the worksheet (near the given
matrix) that has the same dimensions as the answer matrix.

Let's say that we wish to multiply the given matrix of a scalar
of three (3). Since we are multiplying a 4 x 3 matrix by the
scalar, our result will also be a 4 x 3 matrix.

3. Type: = 3*(A3:C6) (This will appear in the formula bar.)

4. Since this answer will result in an array (matrix), you will need to: CTRL+ SHIFT+ ENTER		  
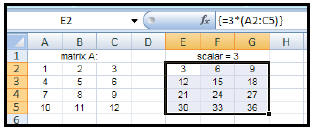How to multiply two matrices:

1. Enter the data of each matrix to be
multiplied.

2. Highlight another section of the worksheet
(near the given matrices) that has the
same dimensions as the answer matrix.

Let's say that we wish to find the product
of matrix A (3 x 3) and matrix B (4 x 3). Recall that the number of columns of the first matrix must be equal to
the number of rows of the second matrix to produce a product matrix . Therefore, we must find the product of
[B] x [A] – which will be a 4 x 3 matrix.

3. Type: = MMULT(E2:G5,A2:C4) (This will appear in the formula bar.)

4. Since this answer will result in an array (matrix), you will need to: CTRL+ SHIFT+ ENTER		  
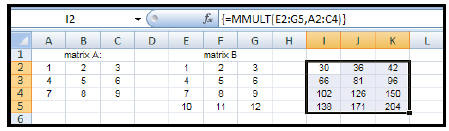How to find the inverse of a square matrix :

1. Enter the square matrix that is to be inverted.

2. Highlight another section of the worksheet (near the
given matrix) that has the same dimensions as the given
square matrix.

Since we were given a 3 x 3 matrix, its inverse will also
be a 3 x 3 matrix.

3. Type: = MINVERSE(A2:C4) (This will appear in the formula bar.)

4. Since this answer will result in an array (matrix), you will need to: CTRL+ SHIFT+ ENTER		  
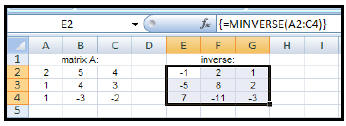How to find the determinant of a square matrix:

1. Enter the given square matrix.

2. Highlight a cell of the worksheet (near the given matrix)
where you wish the answer to appear.

In the diagram at the right, the answer will appear in cell
G2.

3. Type: = MDETERM(A2:C4) (This will appear in the formula bar.)

4. Since this answer will NOT result in an array (matrix) of more than one answer, you may just press ENTER to get the result. (However, if you forget – and do CTRL+ SHIFT+ ENTER, you will get the same result.)		  
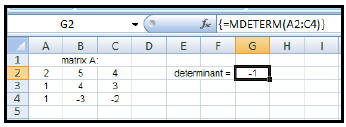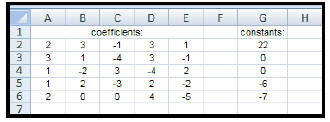
How to use inverse matrices to solve systems of linear equations:
Let's say we wish to solve this system of equations: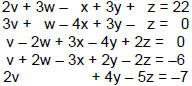
 The matrix equation for this system is: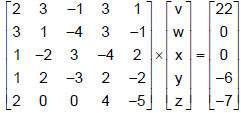
1. Enter the data for the coefficient matrix and the constant
matrix (as shown).

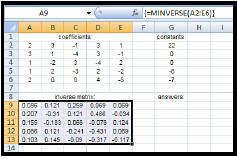
 2. Find the inverse of the coefficient matrix:
• Highlight: cells A9 to E13
• Type: =MINVERSE(A2:E6)
• Remember to CTRL+ SHIFT+ ENTER.
3. Multiply the "inverse matrix" by the constant matrix:
• Highlight: cells G9 to G13
• Type: = MMULT(A9:E13,G2:G6)
• Remember to CTRL+ SHIFT+ ENTER.

The answers to the given system will appear in the
resulting matrix. In the given example, the solutions are:
v = 1, w = 2, x = 3, y = 4, z = 5

Recall: A matrix will have no inverse if its determinant is zero . So, before attempting to find the inverse of a
coefficient matrix, you may want to check the value of its determinant. If the coefficient matrix of a system
of linear equations has a determinant equal to zero, the system will not have a unique solution. And, you
will have to find the general solution by hand – using the Gauss-Jordan Elimination Method .

Prev Next