Algebra Formulas and Notes
| Real Numbers and Their Properties | ||
| Order of Operations: | Please | parentheses, brackets, braces, & absolute values |
| Excuse | exponents | |
| My Dear | multiplication and division (left to right) | |
| Aunt Sally | addition and subtraction (left to right) |
Reciprocal of a is 1 ÷ a and of a ÷ b is b ÷ a a ÷ b = a • 1/b
Multiplication and division:
The answer is positive if both numbers have the same sign.
The answer is negative if the numbers have different signs .
0 ÷ a = 0
a ÷ 0 = undefined
To multiply fractions: divide the product of the numerators by the product of
the denominators.
(a ÷ b) • (c ÷ d) = (a • c) ÷ (b • d) (a ÷ b) ÷ (c ÷ d) = (a • d) ÷ (b • c)
If a ÷ b = c ÷ d, then a • d = b • c
To add fractions: replace each fraction with an equivalent one with a common
denominator
and then add the numerators together.
| a ÷ c + b ÷ c = (a + b) ÷ c | a ÷ c - b ÷ c = (a - b) ÷ c | |
| Properties: | Distributive | a • (b + c) = a • b + a • c |
| Inverse | a + (–a) = 0 and a • 1 ÷ a = 1 | |
| Identity | a + 0 = a and a • 1 = a | |
| Commutative | a + b = b + a and a • b = b • a | |
| Associative | a + (b + c) = (a + b) + c and a(bc) = (ab)c | |
| Multiplication of 0 | a • 0 = 0 | |
If a = b, then a • c = b • c and a ÷ c = b ÷ c.
If a = b, then a + c = b + c and a - c = b - c.
Inequalities:
If a < b, then a • c < b • c and a ÷ c < b ÷ c for c > 0.
If a < b, then a • c > b • c and a ÷ c > b ÷ c for c < 0.
If a > b, then a • c > b • c and a ÷ c > b ÷ c for c > 0.
If a > b, then a • c < b • c and a ÷ c < b ÷ c for c < 0.
Absolute value: |a| = a if a > 0 and –a if a < 0
If |ax+b| = k, then ax+b = k or ax+b = –k. If |ax+b| = |y|, then ax+b = y or
ax+b = –y.
If |ax+b| > k, then ax+b > k or ax+b < –k.
If |ax+b| < k, then –k < ax+b < k.
Graphs, Linear Equations , & Functions
Mid-point of a line is ( [x1 + x2] ÷ 2, [y1 + y2] ÷ 2 )
To find the x-intercept, let y = 0 and solve for x.
To find the y-intercept, let x = 0 and solve for y.
Slope of a line: m = (y2 – y1) ÷ (x2 – x1)
Positive sloped lines rise from left to right.
Negative sloped lines fall from left to right.
Parallel lines have equal slopes.
Perpendicular lines have slopes which are negative reciprocals (their
product is -1).
Slope-Intercept form: y = m • x + b where m = slope and (0,b) is the
y-intercept.
Point-Slope form: (y–y1) = m • (x – x1) where m = slope and (x1,y1) is a
point on the line.
Standard form: a • x + b • y = c where a, b, c are integers and a > 0
Horizontal line: y = b slope is zero and y-intercept is (0,b).
Vertical line: x = a slope is undefined and x-intercept is (a,0).
Quadrants: I is upper right, II is upper left, III is lower left, IV is
lower right
Domain is the set of first or independent values.
Range is the set of second or dependent values.
Distance Formula:
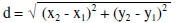
Sum of functions : (f+g)(x) = f(x) + g(x)
Difference of functions: (f-g)(x) = f(x) - g(x)
Product of functions: (f•g)(x) = f(x) • g(x)
Quotient of functions: (f÷g)(x) = f(x) ÷ g(x), g(x) ≠ 0
Exponents and Polynomials
Adding polynomials: Add like terms.
Subtracting polynomials: Change all the signs of the second polynomial
and add to the first.
Multiplying polynomials: Multiply each term of the second polynomial by
each term of the first polynomial and add the
products.
The FOIL method:
1) Multiply the two First terms to get the first term of the answer.
2) Find the Outer and Inner product and combine them to get the middle term of
the answer.
3) Multiply the two Last terms to get the last term of the answer.
| Product rule for exponents : |
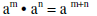 |
Quotient rule for exponents: |
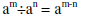 |
| Power rule (a) for exponents: |
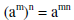 |
Zero Exponent: |
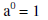 |
| Power rule (b) for exponents: |
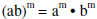 |
Negative exponent: |
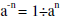 |
| Power rule (c) for exponents: |
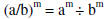 |
Changing from negative to positive exponents:

Scientific Notation: a • 10n where 1 ≤ a < 10 and n is an integer e.g. 8000 = 8 • 103 & 0.0004 = 4 • 10-4
Product of the sum and difference of two terms: (a+b)(a-b) = a^2 - b^2
Dividing a polynomial by a monomial: (a+b) ÷c = a÷c + b÷c
Remainder Theorem: If a polynomial P(x) is divided by (x – a), the
remainder is equal to P(a).
Factoring
Finding the Greatest Common Factor:
1) Write each number in prime factored form.
2) List each prime number or each variable that is a factor of every term in the
list.
3) Use as exponents on the common prime factors the least exponents from the
prime factored forms.
4) Multiply the primes from 3). If there are no primes left after 3), the
greatest common factor is 1.
Factoring by grouping:
1) Collect the terms into two groups so that each group has a common factor.
2) Factor out the greatest common factor from each group.
3) Factor a common binomial factor from the result of 2).
4) If 2) does not result in a common binomial factor, try a different grouping.
Factoring x^2+bx+c:
1) Find two integers (m, n) whose product is c and whose sum is b.
2) Both integers must be positive if b and c are positive
3) Both integers must be negative if c is positive and b is negative.
4) One integer must be positive and one must be negative if c is negative.
5) Factors of the original expression are (x ± m)(x ± n)
Factoring ax^2+bx+c where a
≠1.
1) Find two integers whose product is a • c and whose sum is b.
2) Both integers must be positive if b and c are positive
3) Both integers must be negative if c is positive and b is negative.
4) One integer must be positive and one must be negative if c is negative.
5) Rewrite the expression as ax^2 ± mx ± nx + c and factor by grouping as above.
| Factoring a difference of two squares: |
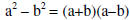 |
[Remember: Not for sum of two squares!] |
| Factoring perfect square trinomials: |
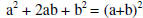 |
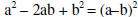 |
| Factoring sum or difference of cubes : |
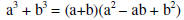 |
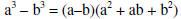 |
| General method for Factoring a polynomial: |
General method for Factoring a polynomial:
1) Is there a common factor?
2) If there are two terms, is it the difference of squares?
3) If there are three terms, is it a perfect square?
4) If there are three terms and the coefficient of the squared term is 1, factor
x^2+bx+c as above.
5) If there are three terms and the coefficient of the squared term is not 1,
Separate the middle term into two terms
with the same sum and then factor by grouping.
6) If there are four terms, try to factor by grouping.
7) Check if any of the factors can be factored further.
Zero-Factor Property: if a • b = 0, then either a = 0 or b = 0 or both
a and b = 0.
Solving a quadratic equation: Write it in standard form (ax^2 + bx + c) =
0 and factor completely.
Set each factor to 0 and solve for x. Check each solution in the original
equation.
Pythagorean formula: In a right triangle, the sum of the squares of the
legs is equal to
the square of the hypotenuse (= the side opposite the right angle; also =
longest side). a^2 + b^2 = c^2
Rational Expressions
Least Common Denominator is the product of all of the different factors
from each denominator,
with each factor raised to the greatest power that occurs in any denominator.
Formulae:
Distance = rate • time
Interest = principal • rate • time
Rate of work = 1 ÷ t (= 1 job per unit of time)
Roots, Radicals and Root Functions
When n is even, principal root
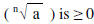 and negative root
and negative root
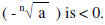
When n is odd, there is only one root
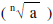 and it can be + or -.
and it can be + or -.
For odd n,
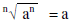 For even n,
For even n,
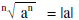
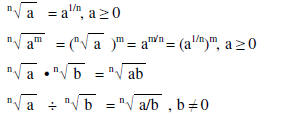
Conjugate of the binomial a + b is a – b
Conditions for a simplified radical:
1. The radicand has no factor raised to a power greater than or equal to the
index.
2. The radicand has no fractions.
3. No denominator contains a radical.
4. Exponents in the radicand and the index of the radical have no common factors
(except 1).
Perfect squares:
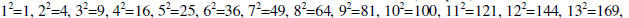
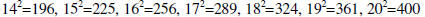
Perfect cubes:
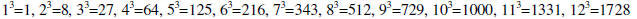
Perfect powers for index n:
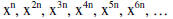
Complex Numbers
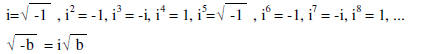
Complex number: a + bi (real part plus imaginary part)
Quadratic Equations
Standard form of a Quadratic Equation: ax^2 + bx + c = 0, a
≠ 0
Discriminant = b^2 - 4ac :
> 0 means 2 distinct, real solutions (rational if a perfect square, else
irrational)
= 0 means 1 real, rational solution
< 0 means two complex solutions
If x^2 = k, then x = ±k
Quadratic formula:
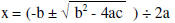
Quadratic Function: Form 1:
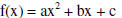
Axis of symmetry: x = -b/2a
Vertex is at the point:
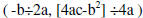
Quadratic Function: Form 2:
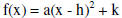
Axis of Symmetry: x = h Y-Intercept: (0,k)
Vertex is at the point (h,k)
Parabola opens up if a > 0, down if a < 0
Exponentials and Logarithms
Exponential function: y = ax where a > 0, a ≠
1.
Solving exponential equations: if ax = ay, then x = y.
Logarithmic function: y = logax means x = ay where a > 0, a ≠
1, and x > 0
logaa = 1 loga1 = 0
Graph of a logarithm passes through (1÷a, -1), (1, 0), and (a, 1)
| Prev | Next |
