Applications of Systems of Linear Equations
| Introduction |
Electrical networks are a specialized type of network
providing information
about power sources , such as batteries, and devices powered by these
sources, such as light bulbs or motors. A power source forces a current to
flow through the network, where it encounters various resistors, each which
requires a certain amount of force to be applied in order for the current to
flow
through.
Systems of linear equations are used to determine the currents through
various branches of electrical networks.
| Known |
Ohm’s Law
• The voltage drop across a resistor is given by V = IR
Kirchhoff’s Law
• Junction: All the current flowing into a junction must flow out of it.
• Path: The sum of the IR terms in any direction around a closed path is
equal to the total voltage in the path in that direction.
| Methods |
We wish to determine the currents I1, I2 and I3 in the
below circuit. Applying
Ohm’s and Kirchhoff’s Law, we can construct a system of linear equations .
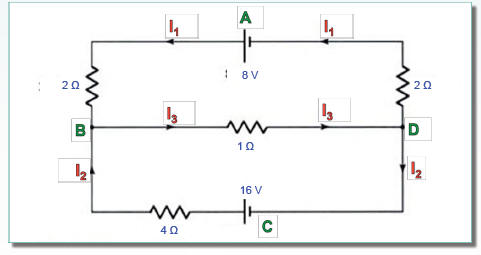
| Results |
Let the currents in the various branches of the circuit be
I1, I2 and I3 . Applying Kirchhoff’s
Law, there are two junctions in the circuit namely the points B and D. There are
two closed
paths ABDA and CBDC. Applying Kirchhoff’s Law to the junctions and paths results
in:
JUNCTIONS:
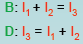
These two equations result in a single linear equation :
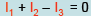
PATHS:
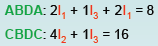
We know have a system of three linear equations in three
unknowns .
The problem thus reduces to solving the following system of three linear
equations in three
variables :
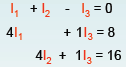
This given system can be placed into an augmented matrix.
We can now use row reduction
algorithms to obtain an equivalent augmented matrix.

| Summary |
From the equivalent row reduced augmented matrix, it is
apparent
the system is consistent and thus a solution exists . The currents I1,
I2 , I3 are as follows
The solution can be verified by substituting the values of
the current
into the original three linear equations with three unknowns.
| Conclusion |
The model for current flow is linear precisely because
Ohm’s Law
and Kirchhoff’s Law are linear: the voltage drop across a resistor is
proportional to the current flowing through it (Ohm), and the sum of
the voltage drop in a loop equals the sum of the voltage sources in
the loop (Kirchhoff).
In practice, electrical networks can involve many resistances and
circuits. Determining currents through branches involves solving
large systems of equations that would require a computer.
| Prev | Next |