Approximate Trisection of an Angle

Given any acute angle Ø ( between 0 and π/2 ), let T := tan(Ø) , so T > 0 . Trisecting Ø by
a finite construction using only a compass and an unmarked straightedge is a problem known to be
equivalent to solving the cubic equation
ƒ(t, T) := (3 – t^2)t – (1 – 3t^2)T = 0

for a positive root t = tan(Ø/3) < 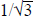by using only finitely many arithmetic operations drawn
from the set 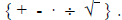Here “equivalent” means that any solution of either problem can
be translated routinely into a solution of the other. However, except for some special values of T
like T = 1 but not T = 2 nor T = 3 , no such solution exists; this was proved by P. Wantzel in
1837. His proof can be found in several books; for example, What is Mathematics by Courant
and Robbins, Galois Theory by I. Stewart, and Famous Problems of Elementary Geometry by
Felix Klein, transl. by W.W. Bemer & D.E. Smith, 2d ed., rev. by R.C. Archibald (1930),
republished (1955) by Chelsea Publ. Co., New York. U. Dudley’s book A Budget of Trisectors
dissects many failed attempts to trisect angles using only a compass and unmarked straightedge.

No fatal flaw in Wantzel’s proof has come to light. None the less, now and then someone will
dispute that proof’s correctness and claim to have solved the trisection problem. A complicated
construction may be presented, sometimes with an alleged proof of validity, often with many
examples showing how well it works. Then the mathematical community will be challenged to
Acknowledge this solution, or show why it is wrong.

In fact, many finite constructions exist, using straightedge and compass alone, that trisect angles
well enough for every practical purpose; many formulas using only finitely many allowed
operations will, given T , solve the equation ƒ(t, T) = 0 for t well enough for every practical
purpose. However, they are all approximate solutions; and although they approximate so well
that no practical measurement nor inexpensive numerical calculation can discern their error, they
do not refute the impossibility of an exact solution. How is such a state of affairs possible?

Consider solving for t the equation ƒ(t, T) = 0 using only finitely many allowed operations
carrying some preassigned number of decimal digits. For instance, use five-function calculators
to perform the arithmetic. Then a formula that computes t almost as accurately as it can be
displayed requires at most a number of operations proportional to the logarithm of the number of
digits displayed . Doing the job as accurately as possible on another calculator that carries about
twice as many decimal digits is feasible with a formula at most a dozen operations longer.

Here is an example of such a formula, based upon Newton’s iteration for solving ƒ(t, T) = 0 .
Start by computing a crude initial approximation t0 := T/(1.85 + 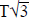) . Then for n = 0, 1, 2, 3,
... in turn compute t_n+1 := F(t_n, T) where
F(t, T) := ( 2t^3 – (3t^2+1)T )/( 3(t^2–1) – 6tT )

until t_n is accurate to almost as many decimals as the calculator displays. Then t₁ is accurate to
over 2 sig. dec., t₂ to over 7 sig. dec., t₃ to over 14 sig. dec., and so on. An error in the 14th
sig. dec is less than the breadth of a wisp of spider’s silk compared with the distance to the moon.
The foregoing formula is one of the easiest to describe but not the shortest that works. In fact, the
shortest formula may be hidden in the obvious formula
t = tan( arctan(T)/3 )

which, though not confined to the allowed set of operations 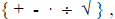is actually
implemented with just those operations plus one more: comparison. In other words, when a
[tan] or [arctan] key is pressed on a scientific calculator that has them , its internal workings
actually compare the input argument against a number of thresholds and select a short formula
from a list of formulas each designed to approximate the desired function with barely adequate
accuracy over a different narrow range of argument values. Modern computers have memories so
capacious that they can hold extensive tables from which they approximate functions like arctan
and tan in a handful of comparison and arithmetic operations reminiscent of what we used to do
without computers when we looked functions up in tables and interpolated ( performing a few
arithmetic operations ) to get just the value needed.

Similar considerations apply to the trisection of an angle by unmarked straightedge and compass
alone. An adequate approximation can be achieved thus: Halve the given angle repeatedly until it
is tiny enough, depending upon the accuracy desired; then trisect the tiny angle approximately by
trisecting the chord instead of the arc of a circle that subtends this angle at the center; then double
the trisected angle as often as the original was halved. There may be shorter constructions that
work, but none so short as using a Protractor or a Nomogram or a Marked Straightedge.

A Protractor is a semicircle marked in 180 or ( if big enough ) 900 equal increments, scribed
onto a transparent plastic sheet, and used to construct and measure angles in Degrees.

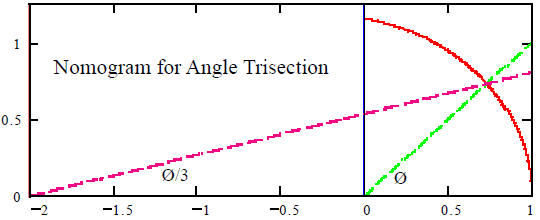
A Nomogram is a curve artfully cut through a transparent plastic sheet and so contrived that an
equation can be solved by intersecting a line or two with this curve . For instance, an angle can be
trisected by laying it at the origin of polar (r, Ø) coordinates with one leg horizontal to the right
and the other prolonged to intersect the curve r = 1/cos(Ø/3) shown below; then draw a straight
line from this intersection to the point 2 units left of the origin on the horizontal axis to intersect
there at a third of the given angle. Each point on this curve can be constructed by a few steps with
straightedge and compass.

A Marked Straightedge is like a yardstick or ruler with marks engraved to measure distance in
fractions of inches or millimeters. Actually, any two marks suffice for the purpose of angle
trisection; this was demonstrated by Archimedes almost 23 centuries ago:

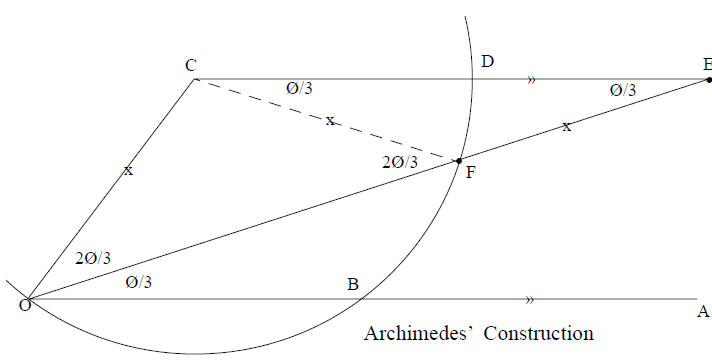
His construction begins by laying out the angle Ø to be trisected; let it be ∠COA . The distance
|CO| is chosen to match the distance between the two marks E and F on the straightedge; this
distance is the radius of a circle centered at C passing through O . Because Ø is smaller than a
right angle, the circle cuts OA again at a point we shall call B . After drawing the circle draw a
line parallel to OA and in the same direction through C to cut that circle at a point we shall call
D . Next comes the tricky part: While one of the straightedge’s marks slides at E along that
parallel line beyond D , slide the other mark at F along the circle from B towards D , sliding
F up until the straightedge passes through O . Now ∠FOA = Ø/3 , thus trisecting ∠COA . The
proof follows from the properties of isosceles triangles ΔOCF and ΔCFE .

Archimedes’ Construction is doubly interesting. First, it accomplishes the trisection quickly
with simple tools. Second, it illuminates an aspect of mathematics that annoys many people:

Ostensibly negligible details can make a big difference.

Without those two tiny marks on the straightedge, the task of trisection is provably impossible.
• • •

In May 2005 David Brooks sent out the following slightly simpler geometrical construction to
trisect an angle using a compass and a draftsman’s unmarked right-angled triangle in lieu of a
straightedge. His construction is illustrated on the next page:

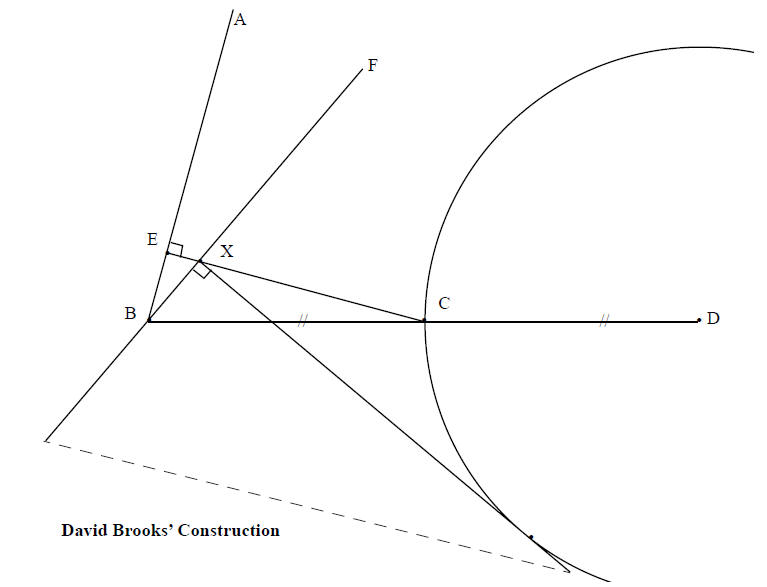
∠ABC is an acute angle given to trisect. (An obtuse angle requires a slightly different figure.)
Extend BC to D so that |CD| = |BC| . Draw a circular arc through C with center D . Drop line
CE perpendicular to BA at E . Slide a right-angled triangle (shown below with its hypotenuse
dashed) into position with its right-angled vertex X on EC , with one adjacent edge through B ,
and with the other adjacent edge tangent to the arc. The edge BX extended to F , say, makes an
angle ∠ABF just one third of ∠ABC , said David Brooks. The justification for his method is
left to the diligent reader.

Because the exact trisection of an angle by compass and unmarked straightedge is impossible, but
easy with other simple tools, and because approximate trisection is not difficult, the trisection
problem no longer offers a path to fame, much less to fortune. Anyone who spends time on the
problem now does so solely for his own amusement.