College Algebra First Day Quiz Solutions
1. Evaluate: 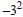
Solution
Reading the expression as “the additive inverse of three-squared” obtains the
correct answer, −9 .
Note the difference that parentheses make: 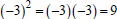
2. Evaluate: 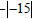
Solution
As for the previous problem , reading the expression as “the additive inverse of
the absolute value of
negative 15” obtains the correct answer, −15 .
3. Simplify: 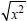
Solution
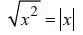
If one used the erroneous identity 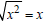 ,
then one would erroneously conclude that
,
then one would erroneously conclude that
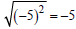 . Recall that the principal square root is
never negative . Using the correct identity
. Recall that the principal square root is
never negative . Using the correct identity
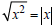 , one would correctly conclude that
, one would correctly conclude that
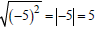 .
.
Note that if the restriction x ≥ 0 is made then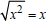 is correct.
is correct.
4. Write a literal equation that defines subtraction .
Solution
Recall that a literal equation (or expression) is one that contains variables
(letters).
a − b = a + (−b)
Example: −7 − 7 = −7 + (−7) = −14
5. What is the geometric meaning of 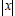 ?
?
Answer: The distance from the origin (zero) to the graph of x on the number line
6. What is the geometric meaning of 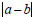 ?
?
Answer: The distance between the graphs of a and b on the number line
7. Find the equation of the line that passes through (−2, 1) and (1, − 2) .
Write your answer in
standard form.
Solution
Standard form of the equation of a line is Ax + By = C . This form can be
obtained from either the
slope-intercept form y = mx + b or the point- slope form
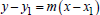 . This solution will use
. This solution will use
the point-slope form as the initial equation.
We are given points on the line, but we are not given the slope. Find the slope
using the slope
equation.
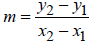
Let P1 = (−2, 1) and P2 = (1, − 2) . (Recall that this is
an arbitrary choice. The opposite choice could
have been made.) Then
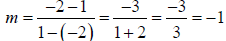
Now let either of the given points be the point
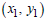 , and substitute the point and the computed
, and substitute the point and the computed
value for the slope into the equation 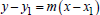 .
Letting
.
Letting 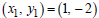 , we obtain
, we obtain
y − (−2) = −(x −1) .
Rearrange this equation to obtain the standard form.
x + y = −1
8. Find the equation of the line that is perpendicular to the line in the
previous problem and also
passes through (1, − 2) .
Solution
Recall that 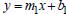 and
and 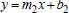 are equations of two lines. The following apply.
are equations of two lines. The following apply.
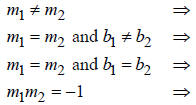 |
The lines intersect at a unique point. |
| The lines are parallel. | |
| The two lines are the same line; i.e., they are coincident. | |
| The lines are perpendicular. |
Because the line in the previous problem has slope m1 = −1, the slope of any
line perpendicular to it
must have slope m2 =1. Substitute this value and the given point into the
point-slope equation to
obtain
y − (−2) =1(x −1) .
The equivalent slope -intercept equation is
y = x − 3 ,
and an equivalent general form equation is
x − y = 3 .
Note that −x + y = −3 is also equivalent general form equation.
9. Simplify:
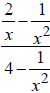
Solution
The given expression is a complex fraction; i.e., it is a fraction that contains
fractions. One way to
simplify it (the way I recommend) is to clear the fractions in the numerator and
denominator of the
main fraction by multiplying both by the LCD of all the fractions that appear in
the numerator and
denominator  .
.
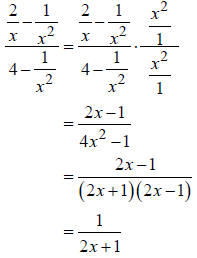
Note that if we had been asked to provide the restrictions
for the identity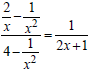 , we would
, we would
state that the identity holds for all real values of x not equal to 0 or −1/ 2 .
( Zero causes the given
fraction to be undefined. −1/ 2 causes the simplified fraction to be undefined.)
Solve: 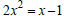
Solution
This is a quadratic equation. Express it in the form
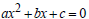 .
.
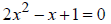
The Quadratic Formula 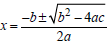 can always be used to
solve any quadratic equation. Let
can always be used to
solve any quadratic equation. Let
us recall some properties of the discriminant 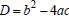 , the radicand in the Quadratic Formula.
, the radicand in the Quadratic Formula.
D > 0 => There are two real solutions.
D = 0 => There is one real solution, of multiplicity two.
D < 0 => There are two complex conjugate solutions.
Another use of the discriminant is that if D is a perfect square, the trinomial
![]() can be
can be
factored over the integers, i.e., using integer coefficients .
Substituting a = 2, b = −1 and c =1 into the Quadratic Formula obtains
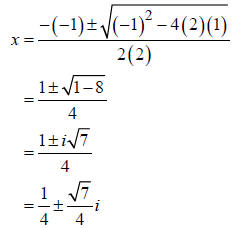
| Prev | Next |