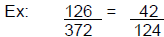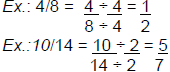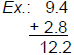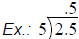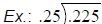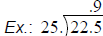Compass Math Sample
The only purpose of this study guide is to give you an
overview
of the type of math skills needed to successfully complete the
Compass math assessment. These sample questions are not
intended to adequately prepare you for the Compass Test.
Fractions
| Adding Fractions: • You need a common denominator (bottom number) • Think of a number that can be divided equally by both of the old denominators NOTE: If you can't think of one, you can always multiply the old denominators to come up with a new "common" denominator • Divide the old denominator into the new denominator, multiply your answer by the old numerator Ex.: 2/4 converts to 6/12 1/3 converts to 4/12 Mixed numbers are OK Ex.: 4 1/3 + 16 1/2 converts to 4 2/6 + 16 3/6 = 20 5/6 |

7. Jack spent 1/3 of an hour on the phone in the morning
and 1/2 of an hour on the
phone in the afternoon. How much time did he spend on the phone altogether?
8. Sandi walked 2 1/4 miles on Monday, 3 miles on Wednesday, and 2 1/2 miles on
Thursday. How many total miles did Sandi walk?
| Subtracting Fractions : • You need a common denominator (see above) Ex.: 2/4 – 1/3 converts to: 6/12 -4/12 = 2/12 = 1/6 • Mixed numbers are OK Ex.: 16 1/2 – 4 1/3 converts to: 16 3/6 – 4 2/6 = 12 1/6 • You may need to borrow from the whole number Ex.: 8 1/6 – 4 5/6 converts to: Borrow 1 from your whole number "8" and add it as a fraction 6/6 to 1/6 = 7/6 7 7/6 – 4 5/6 = 3 2/16 = 3 1/3 |

7. Mark lives 7 1/2 miles from school. Al lives 7 1/8
miles from school. Al lives how
much closer to school than Mark?
8. Greg is 5 6/7 feet tall. His brother, Sam, is 5 3/4 feet tall. How much
taller is
Greg?
| Multiplying Fractions: • No common denominator is needed Ex.: 1/2 x 1/4 = 1/8 • Change mixed numbers to improper fractions Ex.: 2 2/3 x 1/4 converts to: 8/3 x 1/4 = • Multiply the numerators together and the denominators together Ex.: 8/3 x 1/4 = 8/12 = 2/3 ( reduce to lowest terms ) • When your numbers are large Cancel our common factors whenever possible 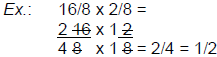 |

7. Mary mailed four packages. Each weighed 7 1/2 pounds.
What was the total
weight of the four packages?
8. Harold needs 2/3 majority of the vote to be elected sheriff. If 1200 people
vote,
how many votes does he need to be elected?
| Dividing Fractions: • No common denominator is needed, Flip the second fraction and multiply Ex.: 1/2 ÷ 1/4 converts to: 1/2 x 4/1 = 4/2 = 2 • Change mixed numbers to improper fractions: Multiple the whole number by the denominator (bottom number) and add it to the numerator (top number) Ex.: 3 3/4 ÷ 9/10 converts to: (3 x 4 = 12 + 3 = 15) 15/4 ÷ 9/10 = 15/4 x 10/9 = 5/2 x 5/3 = 25/6 = 4 1/6 |

5. Cindy and Cathy plan to split 1 2/3 pounds of
chocolate. How much will each
get?
6. The distance from Boston to New York City is 222 miles. If a driving trip
took 4
1/2 hours, what was the average speed per hour?
7. If 15 3/4 pounds of grass seed was used to seed five acres, how much seed was
used per acre?
8. Gilligan's ordered a box of steaks weighing 480 ounces. If the average steak
weighs 7 1/2 ounces, how many steaks were in the box?
| Reducing Fractions: • If both of the last digits are EVEN – divide by 2 • If both of the last digits are ZERO or 5 – divide by 5 • If one of the last digits is ODD – try dividing by 3 • If the sum of the digits in both the numerator & the denominator are divisible by 3 then the numbers themselves are divisible by 3
• Can the larger number be divided by the smaller? |
|||
| DECIMALS Adding Decimals: • Line up your decimal points • Bring the decimal point straight down and add
|

3. Deb sent her son to the store for three items. They
cost $.85, $1.06, and $.35.
How much did he spend?
4. Tom earns $197.25 a week as a word processor. He makes $15.75 in overtime.
What is his week's earnings?
| Subtracting Decimals: • Line up your decimal points. • Bring the decimal point straight down and subtract. 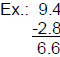 |

3. Find the difference between .010 and .0031?
4. A CD player selling for $125.00 is on sale for $89.99. If Sue purchases the
player
at the sale price, how much does she save?
| Multiplying Decimals: • Multiply the numbers • Count how many numbers are to the right of the decimal point • Starting at the far right of the answer, count over the number of places and place your decimal point in that space Ex.: 4.25 x 8.3 = (There are three numbers to the right of the decimal point.) Multiply: 425 x 83 = 35275 Place Decimal: 4.25x 8.3 = 35.275 |

3. Joyce has a Christmas savings plan. She saves $10.25 a
week for 50 weeks. If she
completes her plan, how much will she save?
4. Carla worked 46 hours this week (40 regular hours and 6 overtime hours). Her
hourly
rate is $7.50 and her overtime rate is $11.25. What is Carla's gross pay for the
week?
| Dividing Decimals: • If there is no decimal in the divisor (the number outside the box), move the decimal in the dividend (the number in the box) straight up into the answer area.
• If there is a decimal in the divisor, move the
decimal point in the dividend to the right
• Place the decimal point in the answer straight up from the location in the dividend.
|

3. A gas station pumped 675.25 gallons of gas in 2.5
hours. How much gas was
pumped in an hour?
4. A developer divided 11.25 acres of land into .25acre
lots. How many lots did he
make?
| Prev | Next |