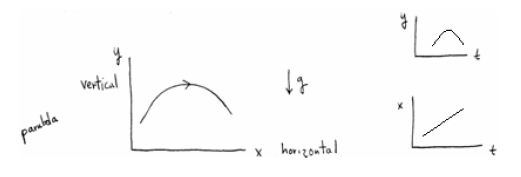
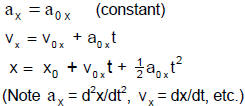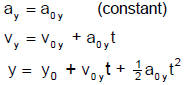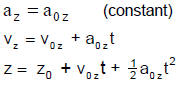Constant Acceleration in any Dimension
Constant Force Means Constant Acceleration in Each Dimension
• Extend Constant Acceleration to all Dimensions
• Gravity Trajectories in 2D (with no Initial Angle)
• Stroboscopic Picture of Trajectories: Motion Snapshots
Let’s prepare ourselves for 2D trajectories:
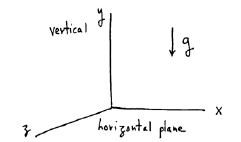
ACCELERATION IN THREE DIMENSIONS
Recall we need three numbers (components) with respect to some
reference point to tell where we are in 3D (actually, this defines 3D.)
We also need three numbers (Cartesian or rectangular coordinates)
each for velocity and acceleration in 3D!
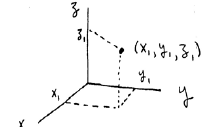
For acceleration components of a body given in all three directions, we can
treat this as three
separate 1D motions. So, if all three acceleration components are constant in
time, we have
similar-looking equations for all three x, y, z coordinates (which give us the
displacements in all
three dimensions). See below where we just add subscripts to distinguish the
three numbers
we need for velocity and acceleration
CONSTANT ACCELERATION FORMULAS FOR ALL COORDINATES
| x coordinate:
|
y coordinate:
|
z coordinate:
|
The above must have come from some constant
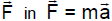 which implies we have constant
which implies we have constant
acceleration
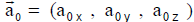 where every acceleration component is constant.
where every acceleration component is constant.
THE CONSTANT SURFACE GRAVITY ACCELERATION g
Ubiquitous Example Of Constant Acceleration
At the surface of the earth (and we’ll learn where we get this in Chapter 4),
gravity
vertically exerts a constant force—so that there is a “downward” constant
acceleration.
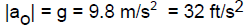

(We use g > 0 always and we put in explicitly any negative sign
that may be
needed in front of g. So, for example, if the y axis is positive upward and
gravity is
downward:
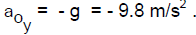
Added note: Most texts use g = 32 ft/s2 = 9.8 m/s2 = 980 cm/s2 in
calculations. (For more
accurate numbers, we need to know the latitude – see later discussions on
“centripetal” effects.)
In SI, one could even use g = 10 m/s2, since it generates only a 2% error!
CONSTANT GRAVITY TRAJECTORY PROBLEMS
Air Friction Neglected for Most of this Course!!!
Quick 1D Trajectory Example:
Note: See Ch 2 for related discussions.
A stone is released from rest, 2 m above ground. How long does it take for
the stone to hit the
ground? (The neglect of air friction is not a bad approximation here.)
Solution: With the usual choice of y for the vertical position (with up to be
the positive y
direction). You can choose other conventions as long as you stay consistent
throughout your
work. In addition, let’s choose the initial time t = 0 where the initial
position is
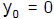 and the
and the
initial velocity is
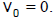 Then for the time thit that the stone hits the ground,
Then for the time thit that the stone hits the ground,
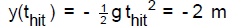
we solve for t (notice how you have to keep track of all the minus signs so
that they cancel out
as they must)

********************************************************************************************
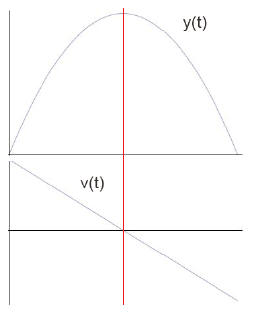
Problem 3-1 To review your old high school stuff, suppose
you throw a ball straight upward with an initial speed of 15 m/s.
You eventually catch the ball when it comes back down. The
plot of its position y(t) is shown on the right and is a good old
parabola symmetric around the vertical red line that goes
through its peak. The velocity v(t) = dy/dt, which is of course
the slope of y(t), is shown in the graph below the y(t) plot.
a) How long will it take to get to the maximum height?
b) How high (relative to your hand) will the ball go?
c) How long does it take for the ball to fall from its
maximum height back to your hand? Don’t use
symmetry but check your answer against (a). (For
posterity, we prove the symmetry below; but don’t use
it, pretty please!)
d) What will the speed of the ball be when you later catch
it in your hand? Again, don’t use symmetry but
compare your answer to the initial value .
********************************************************************************************
Symmetry Proof: We can prove this fast since we can put our origin, y=0, t=0,
at the peak
so that times on the left of the red line are negative. Then, if we can
show y(-t) = +y(t) and v(-t)
= - v(t), for any t, we are done! With y=0, t=0 at the peak, then
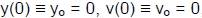 ,
and
,
and
we have y(t) = -1/2gt2 and v(t) = -g t . We immediately see y(-t) =
y(+t) and v(-t) = - v(+t) .
Q.E.D. (You already knew this for a parabola from math class so ... never mind!
- Gilda Radner)
2D Trajectory Formulas:
Now we add the horizontal directions to our motion in constant gravity in the
negative y
(vertical) direction. Therefore,
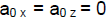 ,
in addition to
,
in addition to
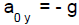 in our boxed
in our boxed
equations of p. 3-1. The corresponding picture is
It is important to note that these three coordinates evolve independent of
each
other and we’ll see the implications of that over and over.
Why do we just talk about 2D instead of 3D in much of our trajectory stuff?
Well, motion
will be in planes (the directions of the initial velocity and gravity determine
a plane to
which the motion will be restricted, so choose the x-y plane for convenience to
be that
plane and we will therefore only need x-y plots from now on!!
We are often interested in y(x) plots to go along with our old time plots,
y(t) and x(t).
The general kinds of plots we get are parabolas for y(t) and straight lines for
x(t). (This
means that y is a quadratic function of t and x is a linear function of t.) We
also get
parabolas for y(x) because if we take the relation x(t) and then solve it for t
in terms of x ,
and then substitute it into y(t), we get y as a quadratic function of x. The
various plots
look like :
The general formulas are
1) For zero acceleration in the x direction, we have the linear relation for x and vx is constant:
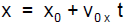 and
and
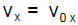 = constant
= constant
2) For acceleration –g in the y direction, we have the quadratic relation for
y
and the linear relation for vy :

Simple 2D Trajectory Example: A stone is thrown horizontally with a
speed 3.0 m/s
from the edge of a cliff
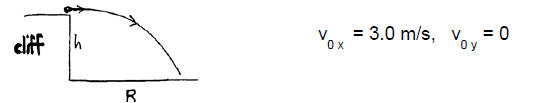
Choose the initial position of stone to be x0 = y0 = 0 at t0 = 0. Suppose it
hits the
ground at t = 2.0s. Where does it hit? That is, what are the h and R shown in
the
figure?
Vertically:
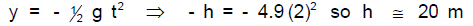

Horizontally:
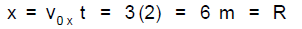
Notice the irrelevance of v0 x (and x) to the h calculation here! You’ll think
about this
kind of thing in the following problem.
********************************************************************************************
Problem 3-2
a) Suppose someone in 2010 shoots marbles horizontally off of one of the
tallest
buildings in the world (in Hong Kong) that is presently under construction and
will
be 490 m high. She will shoot one marble at a horizontal velocity of 10 m/s and
a
second one at a horizontal speed of 20 m/s. Calculate the time it takes each
marble to reach the ground, neglecting as always air drag. Discuss any
interesting aspect you see in your answers (we don’t mean the terrible
possibility
that someone might get hit!).
b) Suppose now she releases two marbles off the first building at the same
time.
One of the marbles is shot off horizontally with a speed of 10 m/s. The other
marble is dropped straight down, without an initial velocity. Use graph paper to
plot the y(x) graphs of the two trajectories. Draw them on the same coordinate
system (i.e., side-by-side). Also indicate on each trajectory with big black
dots
(or purple ones, maybe) the instantaneous position of the marbles at every
second during the fall. Discuss any interesting aspect you see in the drawing of
the dots.
Note: In (b) you’ve just drawn a “strobe picture” of motion—see the Appendix!
********************************************************************************************
APPENDIX: STROBE FLASH PICTURES
“Particle Motion Diagrams”
Let’s extend what we did in part (b) of the previous homework problem by
drawing more “motion
snapshots”—or strobe diagrams. Drawings of objects changing position for a
sequence of
equally-spaced time intervals can be useful for understanding the connections
among position,
velocity, and acceleration.
Consider two cars A and B, where A starts out at a time t1 ahead of B, and
the two cars travel at
constant velocities that are different from each other. Let’s represent the cars
with big black
dots, so that you can easily see how far each car has gone during each time
interval:

The positions of the two cars at times t1, t2,
t3 ... are shown so that, for
example, A is in front of B
at time t1 but behind at t5. The time intervals between the flashes for each car
are chosen to be
equal, and the arrows drawn between each successive position represents the
change in the
car’s position. We see that for constant time intervals, the length of the arrow
connecting
each strobe flash position is proportional to its velocity. So we can compare
the 1D velocities in
such a picture simply by comparing the lengths of the arrows!
Now consider a car that starts from rest and accelerates
to a steady speed for a short distance,
then brakes to a halt. Its strobe diagram looks like

Again, since the strobe flashes are at equal times, the
spacing (the length of any arrow)
between any two dots indicates the relative speed between flashes. We can also
look at the
difference in the lengths of any two successive arrows to approximate the
acceleration at that
time. For example, if an arrow is longer than the arrow just preceding it, we
have an increase in
speed over the two intervals. A shortening of an arrow compared to the previous
arrow indicates
a proportional decrease in speed.
******************************************
Problem 3-3 The figure shows six sequential frames,
1-6, for the motion diagram of two moving
cars, A and B.

(a) Do the two cars ever have the same position at the
same instant of time? If so, identify the
frame number(s).
(b) Do the two cars ever have the same average velocity over the same interval
in time? If so,
identify the frame number(s).
******************************************
| Prev | Next |