Departmental Syllabus for College Algebra
Text: Algebra and Trigonometry custom edition for
FIU (or 8th edition) by Michael Sullivan
Description: The focus of this course is on functions and their properties. In
particular, properties
and graphs of linear , quadratic, rational, exponential and logarithmic functions
are discussed. Ways
of solving systems of equations and inequalities are introduced at the end of
the semester.
Objectives: After finishing the course students should have a good understanding
of the concept of a
function, its domain and range. They should be able to graph basic functions and
be familiar with
their properties. They should be able to perform operations on functions , form
composition and find
the inverse of some one-to-one functions. They should know and be able to apply
properties of
logarithms. They should be able to solve exponential and logarithmic equations
and systems of
equations and inequalities .
Organization of the course: The class meets either twice a week
(Tuesday/Thursday) for 75 minutes
or three times per week (Monday/Wednesday/Friday) for 50 minutes. In a regular
semester there are
about 28 75-minute and 42 50-minute lectures. A suggested pace is outlined
below. The schedule
allows for in-class exams: three 75-minute exams for 2-day schedule and five
50-minute exams for 3-
day schedule. At least two exams must be given before the drop date. The last
exam must cover
exponential and logarithmic functions The 2.5 hour final exam is comprehensive
and mandatory for
all students. All sections will have a common departmental final. The final exam
must count for
25% of the final grade.
The exams are to test students’ knowledge and ability to perform specific tasks,
so open book/notes,
formula sheets/cards are not allowed. Graphing calculators are prohibited in
this course and the
use of scientific calculators should be reduced to minimum .
The suggested homework assignment is attached, but some students might need more
practice so
assign as many problems as you feel is necessary.
Suggested pace
( the number of lectures for a 2-day schedule is given, the corresponding number
for a 3-day
schedule is in parenthesis )
Chapter R - 4.5 (6) lectures
Sec R.2 (objectives 5 and 6 only)
Sec R.4
Sec R.5
Sec R.7
Sec R.8
Chapter 2 - 3 (4) lectures
Sec 2.1
Sec 2.2 (optional : testing an equation for symmetry)
together with 1.2
( when finding intercepts use examples that lead to quadratic equations, review
methods of solving
such equations (factoring, square root method ), then assign homework from both
sections )
Sec 2.3
Sec 2.4 (you can use the general equation of a circle to find intercepts as
means of reviewing solving
equations by using quadratic formula; assign problems from sec 1.2 dealing with
such equations)
Chapter 3 – 6 (8) lectures
Sec 3.1 (make sure to discuss the difference quotient; Ex # 73-80)
Sec 3.2
Sec 3.3 (Optional: local maxima and minima; do not cover objective 5 and the
secant line)
Departmental handout : More on Functions (attached) and Sec 5.4 (review sec 5.4
while covering
departmental handout and then assign homework from the handout and sec 5.4;
problems on the
handout that lead to quadratic equations can be assigned as supplemental HW)
Sec 3.4 (skip greatest integer function)
Sec 3.5
Sec 3.6
Chapter 4 – 2 (4) lectures
Sec 4.3 (emphasize objectives 3 and 4)
Sec 4.4 (objective 1 only)
Sec 4.1 optional (cover objectives 1-3 very briefly)
Sec 4.5 optional (can be combined with 4.4; show 1-2 examples)
Chapter 5 – 1.5 (3) lectures
Sec 5.2 (omit oblique asymptotes)
Sec 5.3
Chapter 6 – 6 (10) lectures
Sec 6.1 (make sure to cover examples 6,7)
Sec 6.2
Sec 6.3
Sec 6.4 (make sure that students understand what a logarithm to the base a of b
is;
 discuss the domain of logarithmic functions)
discuss the domain of logarithmic functions)
Sec 6.5
Sec 6.6 (objectives 1 and 2 only)
Sec 6.7
Sec 6.8 optional (if you omit this section, make sure to assign some word
problems from sec 6.3 and
6.4)
Chapter 12 – 2 (3) lectures
Sec 12.1 (objectives 1-4 only; make sure that students understand what the
solution of a
 dependent system is ; cover some word problems)
dependent system is ; cover some word problems)
Sec 12.6
Sec 12.7
MORE ON FUNCTIONS
For problems 1-19, find the domain of the function
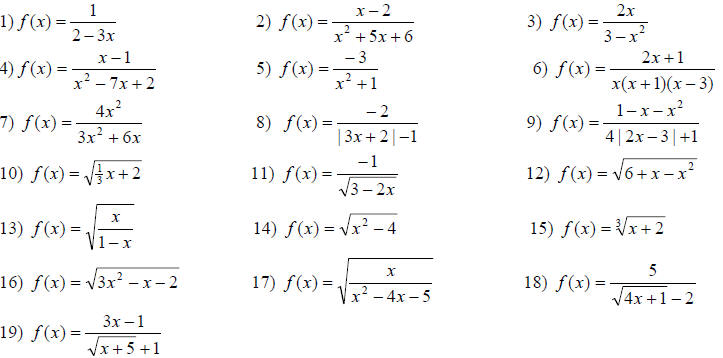
For problems 20-25, find the x-intercepts, if any
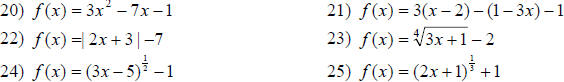
26) Find values of x for which the graph of
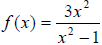 lies below the x-axis.
lies below the x-axis.
27) Find values of x for which the graph of f (x) =| 2x + 3 | lies below the
graph of g(x) = 4.
28) Find values of x for which the graph of f (x) =| 4 − 2x | lies below the
graph of g(x) = 6.
29) Find values of x for which the graph of f (x) =| 7 − x | lies above the
graph of g(x) = 1.
30) Find values of x for which the graph of f (x) =| 5x + 8 | lies above the
graph of g(x) = 2.
ANSWERS
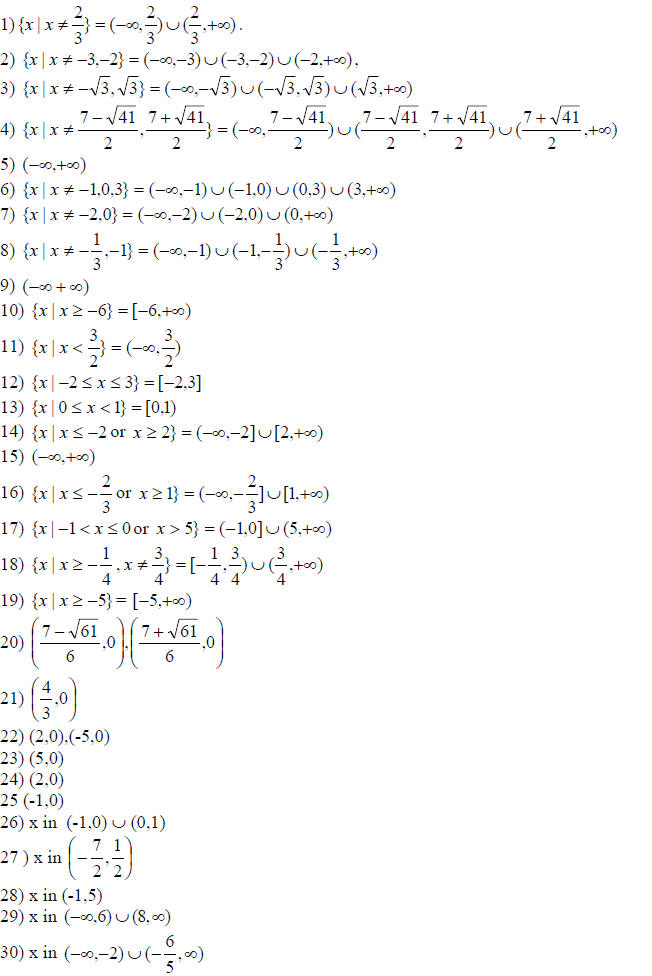
Suggested Homework Assignment
| section | problems |
| R.2 | 73-94, 95, 103, 105 |
| R.4 | 17, 21, 23, 25,29,35,37,39,43, 45,49,55,57,59,67,71,75,79, 84,87,93,95,99 |
| R.5 | 9,11,13,15, 17,21 25,27,33-38,39, 43,45,51, 53,54,57,59,63,86,91,93,95,96,99,105,107, 109,117, 119,121, 123 |
| R.7 | 5,8,11,13,15,19,21,23,25,28,31,33,37,41,43,47,49,51,61-71,73,75,76,81,85,87 |
| R.8 | 7,12,15,17,18,21,23,25,29,31,33,37,41,43,47,48,49,51,53,55-74, 77,81 |
| 2.1 | 11,15,19,24,35,45,47 |
| 2.2 + 1.2 |
11, 21,31,39,40, 41,43, 51-54, 59,61,63,68 find intercepts only unless covering tests for symmetries 13, 15, 21, 29, 31, 21, 42, 47, 55, 79, 85, 89 |
| 2.3 | 13, 21,23, 25,27,29,
37,39,41,43,47,49,53,55,57,61,63,64, 67,69,70,77,83,85,89, 93, 103,104,105 |
| 2.4 | 7,9,11,15,21,23,25,27,31 |
| 3.1 | 15,17,19,21,27,31,32,36,40,43,45,47-60,65,68,70,73,75,79,80,81,87,90 |
| 3.2 | 9,10,11,12,13,18,20,25 |
| 3.3 | 11-20, 21,23,25,27,35,36,42,53 29, if covering extrema |
| 5.4 | 3, 5, 7, 11, 13, 21, 23, 25 |
| 3.4 | 17-38, 41, 42, 43, 47, 49 |
| 3.5 | 7,9,11, 13,19-22,24,25, 29, 35,37,39,44,46,47,51,53,55,65a-e, |
| 3.6 | 1a-c, 7a-b,11a-b, 18 |
| 4.1(optional) | 17,18, 19, 37, 39 |
| 4.3 | 17, 27,3235,41,43,45,47,57, 61,65,81,86 |
| 4.4 | 5,7,9,11,19 |
| 4.5(optional) | 3,7, 9, 11,13,15, 17, 19 |
| 5.2 | 13,15,17,20,23-28a-d,35,36,39, 41-52(omit oblique asymptotes) |
| 5.3 | 7,9, 11, 19,20,23, 33, 35,37 |
| 6.1 | 11,17,21,27, 35,41,49, 53-58 |
| 6.2 | 9,11,17,19,23, 33,37,41,42, 57, 61,65 |
| 6.3 | 11,17,18,37,39,45,49, 50,53, 59,63,67,73,79,97,99 |
| 6.4 | 9,11,15,16,21,23,24,25-36, 37, 43, 45, 47, 51,55,59,71,77,83,87,91,97,99,103,107,117 |
| 6.5 | 9,11,13,15,17,25,29,37,41,43,45,47,49,51,55,57,59,61,63,65,69 |
| 6.6 | 6,9,11,15,16,19,21,23,27,29,31,33,39,41,42,49,53,55,59 |
| 6.7 | 3,5,7,11,15,19,39,43,45, 49 |
| 6.8(optional) | 1,3,5,9,21 |
| 12.1 | 19,25,26,27, 29,30, 57,63,64 |
| 12.6 | 5,7,9,13,15,27,28,29 |
| 12.7 | 11-19,23,25,29,33,37,43,45,47 |
| Prev | Next |