FINDING ZEROS OF POLYNOMIAL FUNCTIONS
The Zeros of polynomial functions of degree three and
higher cannot always be found using simple
"recipes". Some Zeros of polynomial functions are best solved using a computer
software because
the " solution recipes " become extremely complex.
The good news is, some Zeros of polynomial functions can
be found by factoring, if the polynomial
function conforms to certain rules . We find Zeros of a polynomial function by
setting the function
equal to 0.
Examples 1-3 illustrate the concept of Zeros of polynomial
functions using polynomial functions of
degree two (quadratic functions).
Example 1:
Find the Zeros for 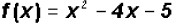 . Since the degree of the
polynomial is two, we must find two
. Since the degree of the
polynomial is two, we must find two
Zeros, not necessarily distinct.
We find the Zeros by setting the function equal to 0 and solve for x.
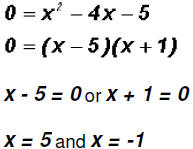
The Zeros of the function are -1 and 5. They are real
Zeros, therefore, they show up on the graph of
the function as x-intercepts.
Example 2:
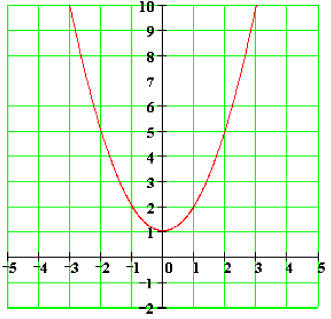
Find the Zeros for 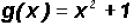
Since the degree of the polynomial is two, we must find two Zeros , not necessarily distinct
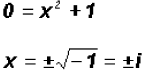
The Zeros of the polynomial are -i and i. You cannot see
the imaginary Zeros on the graph of the
function below.
Example 3:
Find the Zeros for 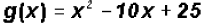
Since the degree of the polynomial is two, we must find two Zeros, not necessarily distinct.
0 = (x - 5)(x - 5)
x - 5 = 0 or x - 5 = 0
and x = 5
In this case, 5 is a Double Zero or a Zero of multiplicity
2. Since 5 is a real number, it is also an xintercept
of the graph of the function .
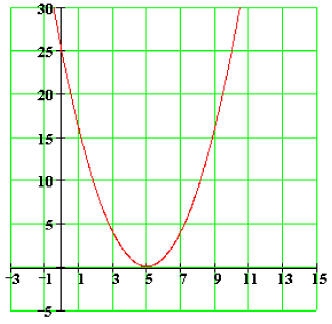
Let's look at the graph of 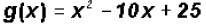
Notice that the x- intercept is also the vertex point as well as the Zero of the quadratic function.
Example 4:
Find the Zeros of the polynomial function 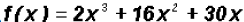
Since the degree of the polynomial is three, we must find three Zeros, not necessarily distinct.
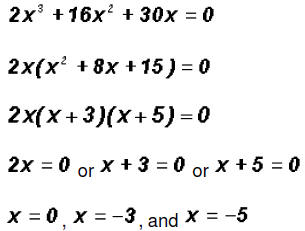
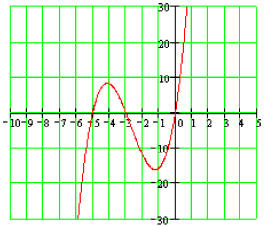
The Zeros are -5, -3, and 0. They are also the x-intercepts of the function.
Example 5:
Find the Zeros of the polynomial function 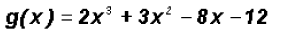
Since the degree of the polynomial is three, we must find three Zeros, not necessarily distinct.
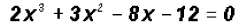
In this case, factoring is not readily apparent. Here, we
will try to group two terms and then we will try
to factor the common factor out of the first two terms and out of the last two!
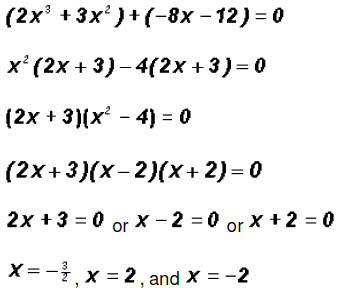
The Zeros are -2,-3/2 , and
2. They are also the x-intercepts of the function.
Example 6:
Find the
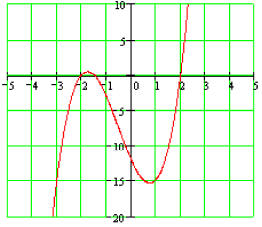
Example 6:
Find the Zeros of the polynomial function 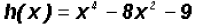
Since the degree of the polynomial is four, we must find four Zeros, not necessarily distinct.
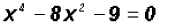
We can factor the equation as follows :
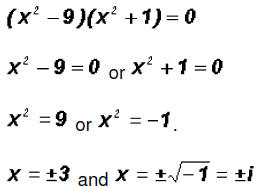
The Zeros are -3, 3, -i, and i. The two real Zeros are the
x-intercepts of the function. The two
imaginary Zeros are not x-intercepts, however, they still help influence the
shape of the graph.
Example 7:
Let's find the Zeros of the polynomial function
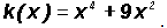 .
.
Since the degree of the polynomial is four, we must find four Zeros, not
necessarily distinct.
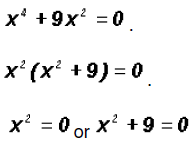
Solving the first factor, we find that x = 0
Solving the second factor, we find that x = -9, which
results in
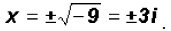
The Zeros are 0 (multiplicity 2), -3i, and
3i. The real Zero is the x-intercept of the function. The two
imaginary Zeros are not x-intercepts, however, they still help influence the
shape of the graph.
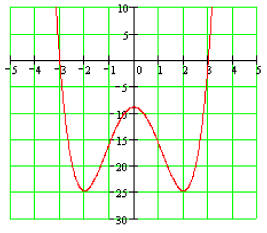
Example 8:
Let's find the Zeros of the polynomial function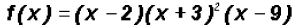
Notice that this polynomial function is already factored.
It is written as the product of its linear
factors. It has degree four.
NOTE: There are two factors, x - 2 and x - 9, which have
degree 1 each, and there is
one factor, x + 3, which has degree 2. When a polynomial function is in factored
form,
we simply add the degrees of each factor. In our case, we get 1 + 2 + 1 = 4.
Since we already have factors, we set each one of them equal to 0,
x - 2 = 0 or (x + 3)2 = 0 or x - 9 = 0
and by solving we find that
x = 2, x = -3,and x = 9
The Zeros are -3 (multiplicity 2), 2, and 9. They are also the x-intercepts of the function.
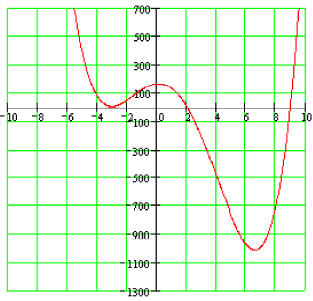
Example 9:
Let's find the Zeros of the polynomial function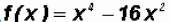
Since the degree of the polynomial is four, we must find four Zeros, not necessarily distinct.
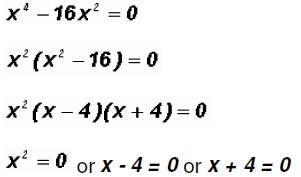
Solving the first factor, we get
x = 0
Solving the second and third factor, we get
x = 4 and x = -4
The Zeros are 0 (multiplicity 2), - 4, and 4. They are also the x-intercepts of the function.
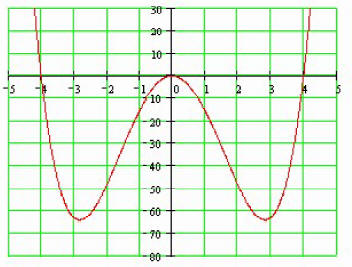
Example 10:
Let's find the Zeros of the polynomial function 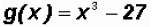
Since the degree of the polynomial is three, we must find three Zeros, not necessarily distinct.
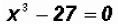
Notice that we are dealing with a Difference of Cubes !
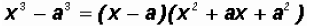
In our case, a = 3, therefore, we can factor as follows
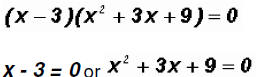
Solving the first factor, we get
x = 3
Solving the second factor using the Quadratic Formula , we get
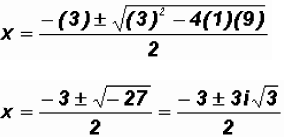
The Zeros are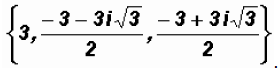 The real
Zero is the x-intercept of the function.
The real
Zero is the x-intercept of the function.
The two imaginary Zeros are not x-intercepts, however, they still help influence
the shape of the
graph.
Please note that it is customary and standard to place the
imaginary number i in
front of radicals instead of after them as is done with rational numbers. See
Example 7 above!
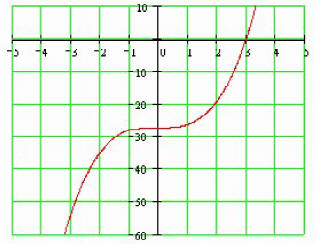
Please observe the following:
Given x3 - 27 = 0, we could also rewrite this as
x3 = 27 and then raise both
sides to
the one- third power :
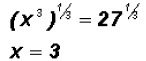
Using this method did not allow us to find the imaginary
Zeros, which we know must exist
because the polynomial is of degree 3!
Example 11:
Let's find the Zeros of the polynomial function 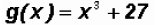
Since the degree of the polynomial is three, we must find three Zeros, not necessarily distinct
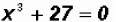
Notice that we are dealing with a Sum of Cubes !
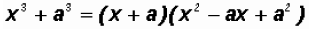
In our case, a = 3, therefore, we can factor as follows
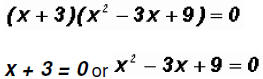
Solving the first factor, we get
x = -3
Solving the second factor using the Quadratic Formula, we get
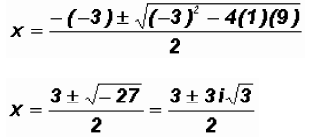
The Zeros are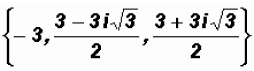 The real
Zero is the x-intercepts of the function. The
The real
Zero is the x-intercepts of the function. The
two imaginary Zeros are not x-intercepts, however, they still help influence the shape of the graph.
Please note that it is customary and standard to place the
imaginary number i in
front of radicals instead of after them as is done with rational numbers . See
Examples 7 and 10 above!
| Prev | Next |