Fractions and Rational Numbers
• A rational number is a real number which can be represented as a quotient
of two integers .
• Rational numbers are exactly those real numbers having decimal expansions
which are periodic or
terminating.
Definition. A rational number is a real number which can be written as
a/b, where a and b are integers
and b ≠ 0. A real number which
is not rational is irrational .
Example. If p is prime, then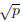 
is irrational. To prove this, suppose to the
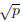contrary that is rational. Write 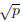= a/b, where a and b are integers
and b ≠ 0. I may assume that (a, b) = 1 — if not, divide out any common
factors.
Now
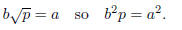
Since p | a^2 and p is prime, p | a. Write a = pc. Then
Now p | b^2, so p | b. Thus, p is a common factor of a and b contradicting my
assumption that (a, b) = 1.
It follows that 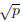is irrational.
More generally, if
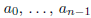are integers, the roots of
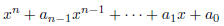
are either integers or irrational.
If b is an integer such that b > 1, and a is a real number between 0 and 1
(inclusive), then a can be
written uniquely in the form
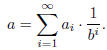
This is called the base b expansion of a. Rather than proving this fact, I’ll
merely recall the standard
algorithm for computing such an expansion: Subtract from a as many
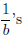as possible, subtract as many
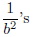from what’s left, and so on.
Here is a recursive procedure which generates base b expansions:
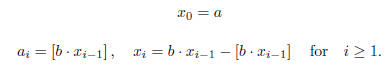
To see why this corresponds to the standard algorithm, note that at the first
stage I’m trying to find
k ≥ 0 such that
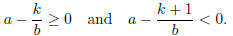
These equations are equivalent to
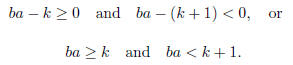
That is, k = [ba], and a corresponds to xi.
It’s convenient to arrange the computations in a table, as shown below.
Example. Find 0.4 in base 7.
I fill in the rows from left to right. Starting with an x, multiply by b = 7
to fill in the third column.
Take the greatest integer of the result to fill in the a-column of the next row.
Subtract the a- value from the
last bx-value to get the next x, and continue. You can check that this is the
algorithm described above.
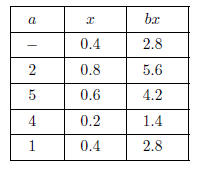
The expansion clearly repeats after this, since I’m getting 0.4 for x again. Thus,
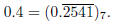
Definition. The decimal expansion
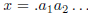terminates if there is a number N > 0 such that an = 0
for n ≥ N.
In this case,
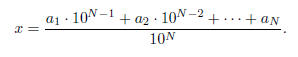
Hence, x is rational.
A decimal expansion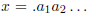 
is periodic with period
k if there is a positive integer N such that
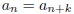for all n ≥ N.
Periodic expansions also represent rational numbers.
Again, I’ll give an example rather than writing
out the unenlightening proof.
The converse is also true: Rational numbers have decimal expansions which are
either periodic or
terminating.
Example. Expres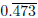s 
as a
rational number in lowest terms .
Since the number has period 3, I multiply both sides by 10^3:
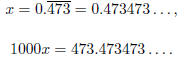
Next, subtract the first equation from the second :
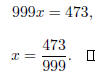
Example. Express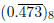 
as a
(decimal) rational number in lowest terms.
Since the number has period 3, I multiply both sides by
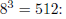
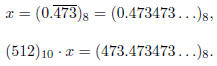
Next, subtract the first equation from the second, being careful about the bases:
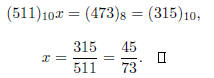
Example. Expres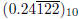s 
as a
rational number in lowest terms.
Since the number has period 3, I multiply both sides by 10^3
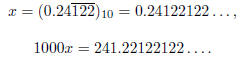
Next, subtract the first equation from the second:
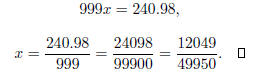
| Prev | Next |