Grade 8 Math
| Idaho Department of Education Content Standards |
Objective | Sub Objectives | Task Analysis | Essential Vocabulary | Sample Assessment |
| Standard 2: Concepts and Principles of Measurement | |||||
|
Goal 2.1: Understand and use U.S. customary and metric measurements. |
8.M.2.1.1 Select and use appropriate
units and tools to make formal measurements in both systems.
CL: C |
• Select and use appropriate units
and tools to make formal measurements in both systems |
• determine appropriate customary and
metric units for given objects • use appropriate tools for measurement in customary and metric system |
• capacity • volume • liter • meter •
gram • milli- • centi- • kilo- |
• Measure the length of your pencil
to the nearest centimeter. • What unit of measure would you use to find the capacity of a cereal box? |
| 8.M.2.1.2 Apply estimation of measurement to
real -world and content problems using standard measuring devices. CL: |
• Apply estimation of measurement to real-world
and content problems using standard measuring devices |
• select an appropriate unit of measure for the
problem • demonstrate magnitude of measurements |
• magnitude | • About how many meters long is a classroom? • Which is more- a kilometer or a mile? |
|
| 8.M.2.1.3 Compare the differences and
relationships among measures of perimeter, area, and volume (capacity) within both systems. CL: |
• Compare the differences and relationships among measures of perimeter, area, and volume (capacity) within both systems |
• identify linear units for perimeter, square
units for area, and cubic units for volume |
• perimeter • area • volume • capacity • square
units • cubic units • dimensions |
• Compare the perimeter and area of a square with
3½" sides. What is the volume of a cube with the same dimensions? |
|
| 8.M.2.1.4 Given the formulas, find the
circumference, perimeter, or area of triangles, circles, and quadrilaterals, and the volume and surface area of rectangular prisms. CL: C |
• Calculate the circumference and area of circles
given formulas • Calculate perimeter and area of triangles and quadrilaterals given formulas • Calculate the volume and surface area of rectangular prisms given formulas |
• select and apply formulas to determine
circumference or area of circles given either diameter or radius • produce answers in terms of pi and using approximations of pi • select and apply formulas for area and perimeter of triangles and quadrilaterals • combine formulas to solve composite area problems • select and apply formulas for surface area and volume of rectangular prisms |
• radius • diameter • circumference • in terms of
pi • quadrilateral • base • height (altitude) • rhombus • trapezoid • parallelogram • prism • lateral area • surface area |
• Use the formula C=πd or C=2πr to find the circumference of a circle with a radius of 3.2 cm. Leave your answer in terms of pi. • Use the formula A=½bh to find the area of a triangle with a height of 7 inches and a base of 12 inches. • Use the formula V=lwh to find the volume of a rectangular prism that is 2 cm x 3 cm x 5cm. |
|
| 8.M.2.1.5 Convert units of measurement within
each system in problem solving situations. CL: C |
• Convert units of measurement within each system
in problem solving situations |
• examine units of measure to determine agreement • determine appropriate unit to use • convert measurments |
• see 8.M.2.1.1 | • Sal has a garden that is 5 yards by 8½ feet. He
wants to put a fence around it. How many feet of fence does he need to buy? |
|
| 8.M.2.1.6 Solve problems involving area of
circles and the perimeter and area of rectangles and triangles.
CL: C |
• Solve problems involving area of circles and
the perimeter and area of rectangles and triangles. |
• apply concepts of area and perimeter to solve
real world problems |
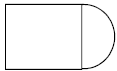
• Kendall needs to paint this basketball key
which is made up of a rectangle and a semicircle. The length of the rectangle is 18 feet and the width is 12 feet. What is the area of the space that needs to be painted
|
||
| 8.M.2.1.7 Use appropriate vocabulary and
notations. CL: Calc: Content Limit: Assessed in the classroom, not on the ISAT. |
• Use appropriate vocabulary and notations | • determine appropriate labeling of perimeter,
area and
volume • communicate using correct mathematical terminology |
|||
|
Goal 2.2: Apply the concepts of rates, ratios, and proportions. |
8.M.2.2.1 Use rates, proportions,
ratios, and map scales in problem-solving situations. CL: C |
• Use rates, proportions, ratios, and
map scales in problem-solving situations. |
• relate data as rates, ratios, and
proportions • use proportions to solve problems involving scale • convert units of measurement as necessary |
• proportion • ratio • scale drawing • unit rate | • During a 7.5 hour drive, a car's
odometer (milage indicator) starts at 18,560 miles and ends at 18,980 miles. What is the car's rate of travel? |
| 8.M.2.2.2 Determine unit rates in real-world
situations. CL: C |
• Determine unit rates in real-world situations | • write and use unit rates to solve problems | • unit rate | • A 32 ounce container of yogurt costs $2.69. An
8 ounce container of yogurt cost $0.75. Find the unit costs of each container. Which is the better buy? |
|
| Goal 2.3: Apply dimensional analysis. | 8.M.2.3.1 Illustrate the
interrelationship of measurement units through dimensional analysis conversions. CL: C, D |
• Demonstrate the relationship
between measurement units through dimensional analysis conversions |
• identify common unit conversions • use appropriate conversion ratios to relate equivalent measurement units |
• conversion ratio (factor) | • Use dimensional analysis to convert
9 kilometers to meters. • Use the correct conversion factor to convert 70 ounces to pounds. |
| Prev | Next |