How to Calculate Eigenvectors and Eigenvalues in Matlab
While calculating things sure is fun, sometimes we need to
choose efficiency over
diversion. This note describes the basics of matrix creation, manipulation, and
other matrix operations in Matlab . For more help, you can type: " help elmat"
in the Command Window for a list of elementary matrix operations , and "help
matfun" in the Command Window for a list of matrix functions. Clicking on
any entry in these lists takes you to a brief description of the Matlab command.
More help is available from the "Help" menu in the menu bar.
In what follows, I have copied and pasted what I typed from the Command
Window. You will only type what follows the Command Window prompt:
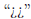 . Every line is ended by a carriage return.
If you see lines that don't start
. Every line is ended by a carriage return.
If you see lines that don't start
with the prompt, they were produced by Matlab.
Basics: How to generate a matrix and access its entries.
Make an m n matrix, A, with all zero entries : "A = zeros(m,n)". For example:
>> A= zeros (3,2),
>> A
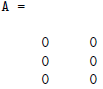
The i, jth entry of a matrix A is accessed by typing "A(i,
j)". For example:
>> A(2,1)=5
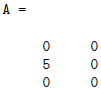
You can define a matrix by typing in the entries,
surrounded by SQUARE
brackets . Semi-colons are used to define a new line. For example:

You can access a single row or a single column by using
the short cut: " : " ,
which means "all indices in this row or column". For example, to see the first
row of B or the second column of B:
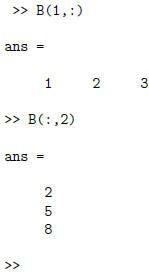
To see the second through third entries of the third row of B:
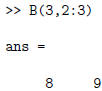
To generate a 5 by 6 matrix of ones:
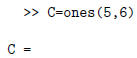
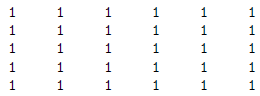
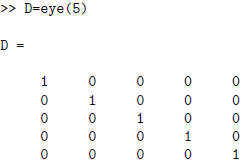
To generate the 5 by 5 identity matrix:
To find the eigenvalues and eigenvectors of a matrix: (I
first define the matrix
given in Problem 19, Section 6.3)

The matrix v is a matrix whose columns are the
eigenvectors of A corresponding
to the eigenvalues given as the diagonal elements of the matrix e. The eigen-
vectors are normalized so they have norm one. If you don't want this, you can
use the 'unbalanced' option:

Sometimes the unbalanced version looks more like the
numbers you would cal-
culate by hand (if you're checking!). You can extract the eigenvalues from the
matrix and store them in a vector using:
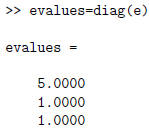
The trace, determinant, and inverse of a matrix are calculated using :
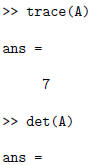
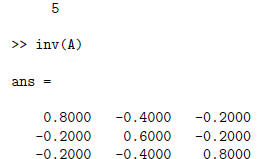
Matrix multiplication is performed using the usual "*"
command. Element-by-
element multiplication ( or division ) can be done using the ".*" command:
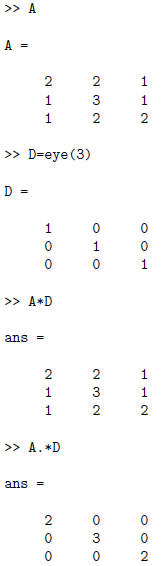
That should get you started!
| Prev | Next |