Inequalities
Like equations there are procedures for solving inequalities. Some of these are exactly the same as equations, some are not. The following chart details the similarities and differences.
| Equations | Inequalities |
| Add or Subtract anything on both sides | Add or Subtract anything on both sides |
| Multiply or Divide anything on both sides | Multiply or Divide any POSITIVE number on both sides. If you Mult. Div. a negative number you must reverse the inequality. |
| Can use properties like Priciple of Zero Products, Principle of Zero Quotients, Principle of Powers … | Can use sign charts , rules for absolute value, test points |
____________________________________________________________________
Solving Linear Inequalities
To solve linear inequalities the procedure is virtually the same as for linear equations. The only difference is that you must be careful when multiplying or dividing on both sides.
EX.
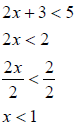
Here dividing is the same because 2 is a positive number.
EX.
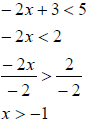
Notice that when I divided by -2 the inequality reversed because -2 is a negative number.
Nonlinear Inequalities
To solve nonlinear inequalities, the standard approach is to use a sign chart. To do this:
1.) Get everything on one side
2.) Factor, or reduce fractions until the inequality is composed of
multiplication and
division of linear or irreducible factors on one side , and zero on the other.
3.) Determine where signs can change (zeros and undefineds).
4.) Create chart with one row for each factor, and one column for each region
between
zeros and undefineds .
5.) Determine the sign of each factor in each region to fill in chart.
6.) Add a final row representing the product /quotient of all factors, and fill
in.
EX. Solve the following inequality.
x2 + 5x + 4 < 0
( x + 1 ) ( x + 4 ) < 0
The zeros are -1 and -4.
| Factor | -inf to -4 | -4 to -1 | -1 to inf |
| x+1 | - | - | + |
| x+4 | - | + | + |
| Product (x+1)(x+4) |
+ | - | + |
The last line gives the sign of the expression on the left. In this case we want to know where this is less than zero, or where it is negative. The only region which satisfies this is -4 to -1. So the answer in interval notation (-4,-1).
| Prev | Next |