INTEGER AND RATIONAL NUMBERS

Theorem 7.7 The ordering of rational numbers is well defined.

Proof Let [x, y] = [a, b], [z,w] = [c, d], and [x, y] < [z,w] with b, d, y, w >
0. We thus have

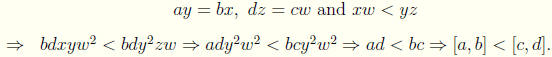
Hence the ordering is well defined.

We define addition and multiplication as follows,

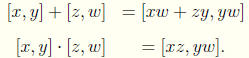
Theorem 7.8 Addition and multiplication of rational numbers are well
defined.

Proof Let [x, y] = [a, b] and [z,w] = [c, d].

For addition we have

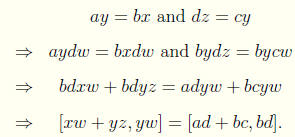
Hence addition is well defined.

For multiplication we have

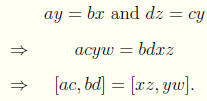
Hence multiplication is well defined.

Just as there is a natural embedding of the natural numbers into the
integers , there is the natural embedding of the integers into the rational
numbers given by the injection,



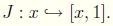
It is easy to verify that this injection is an embedding.

A Field

We leave it the reader to verify the following properties of Q .

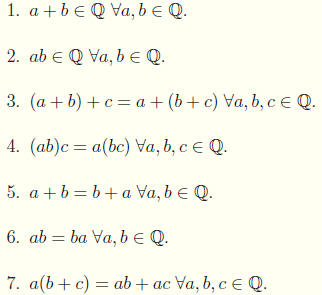
8. 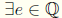such that a + e = e + a =

9. 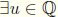such that au = ua =

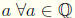
10. 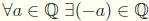such that a + (-a) = (-a) + a = 0

11. 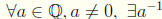such that aa^-1 = a^-1a = 1

The first 10 properties are identical to the properties of an Integral Domain.
Property 11* is replaced by property 11 where a^-1 is called the multiplicative
inverse, or reciprocal .

Any set with two binary operations satisfying these 11 properties is called
a Field.

Exercise Show that every field is an integral domain. That is to say, every
field has no zero divisors .

Differences and Quotients

Definition The difference between integers or rational numbers a and b
is a + (-b), which is written a - b.

Definition The quotient of two rational numbers a and b is a · b^-1, which
is written .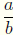

We can see that difference and quotient can be regarded as a binary oper-
ations, we also notice that neither operation is commutative nor associative.
Exercise For any two rational numbers p < q, show that .

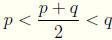Exercise Show that

1. If p, q, r are rational numbers where p ≤ q and r > 0, then pr ≤ qr.

2. If p, q, r are rational numbers where p ≤ q and r < 0, then pr ≥ qr.

3. If p and q are positive rational numbers, then :

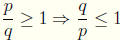Mathematical Induction

The next theorem is a special case of transfinite induction, that is widely
used in many situations. Before we state and prove the theorem we need two
small lemmas that we present as exercises .

Exercise 1. Define the map Ø : N → by Ø(a) = [a + 1, 0]. Show that

Ø(a) + 1 = Ø(a + 1).

Exercise 2. Show that is order isomorphic to ω.

Theorem 7.9 The Principle of Mathematical Induction If 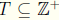 such
that the following conditions are true:

i. 1 ∈ T

ii. if k ∈ T, then k + 1 ∈ T,

then T = .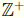

Proof Consider the order preserving bijection Ø : ω → 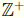defined by
Ø(a) = [a + 1, 0]. Let A = Ø^-1(T). Let x ∈ ω such that S(x) 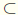A.

If x = 0, then Ø(x) = 1 ∈ T => x ∈ A. If x ≠ 0, then

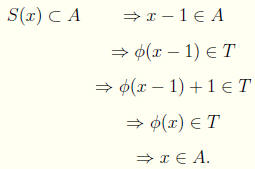
Thus by Transfinite Induction .

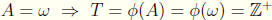The Cardinality of Integers and Rational Numbers