Introduction, Basics, Matlab
3 Calculating Definite Integrals
Another good example of the difference between numerical computation and
analytic techniques is
found in the calculation of definite integrals. Recall that the definition of
the definite integral of a
continuous (and we will assume positive) function f(t) over the interval [a, b],
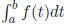 is the area
is the area
under the curve , as shown in Figure 3.
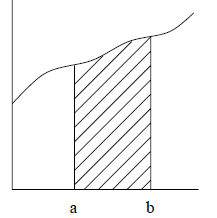
Figure 2: The Definite Integral of f(t) over [a, b]
What is the best way to calculate the definite integral? Our experience in math
classes suggests
that we might use the anti-derivative, that is a function F with F' = f:
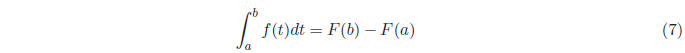
But this technique raises two important questions:
1. How do we determine an anti-derivative function?
2. How difficult is it to evaluate the anti-derivative function at a and b?
The answer to the first question may seem simple - we all learned to calculate
anti-derivatives
in calculus class. But we recall from the same classes that are many situations
in which we do not
have a simple rule for determining the anti-derivative.
There are, likewise , many examples of anti-derivative functions that are more
difficult to evaluate
than the original function, for example:
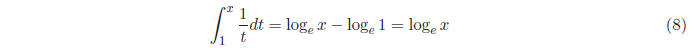
So is there a method for calculating the definite integral
that uses only information we already
know about the function - namely, the value of f at any given point? The answer
is yes, and the
key is to use the definition of the definite integral to approximate its value,
as shown in Figure 3.
We start by splitting up the interval into subintervals of equal size h, then
estimating the definite
integral over each subinterval, then adding them all together. If we split the
interval [a, b] into N
subintervals of equal width 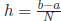 , we can calculate the definite integral as:
, we can calculate the definite integral as:
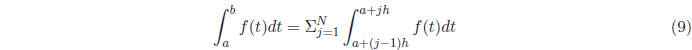
We have reduced the problem to estimating the definite
integral over smaller subintervals. Here
are two possible strategies for estimating the smaller definite integrals:
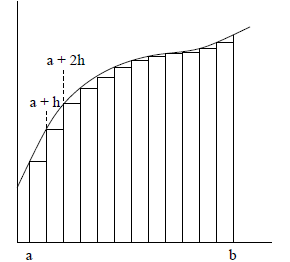
Figure 3: Approximating the Definite Integral Using
Subintervals
Rectangle Rule
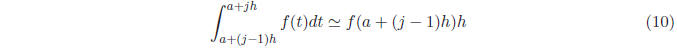
In the rectangle rule, we calculate the area of the
rectangle with width h and height determined
by evaluating the function at the left endpoint of the interval.
Midpoint Rule
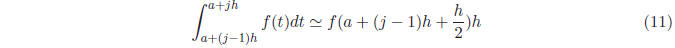
In the midpoint rule, we calculate the area of the
rectangle with width h and height determined
by evaluating the function at the midpoint of the interval
 |
|
| Rectangle Rule | Midpoint Rule |
Figure 4: The Rectangle and Midpoint Rules
These two methods are depicted in Figure 3. Using these methods, we can
calculate the definite
integral by simply evaluating the original function at a number of points , which
we should always
be able to do (otherwise, we don’t know what the function is). We can control
the precision in each
case by changing the size of the subintervals h (and therefore increasing the
number of subintervals).
The smaller the subinterval, the greater the precision.
The next question is, how can we decide which of these
algorithms to use? It seems that the
midpoint rule would be a better choice (Q: why?), but how can we justify this
suspicion?
4 Evaluating Numerical Algorithms
We evaluate numerical algorithms using 3 major criteria:
Cost - The amount of time (usually calculated as the number of operations ) the
computation will
take.
Speed - How quickly the algorithm approaches our desired precision. If we define
the error as the
difference between the actual answer and the answer returned by the numeric
algorithm,
speed is often measured as the rate at which the error approaches 0. The rate is
measured
in terms of some quantity that’s relevant to the problem at hand, such as one
evaluation of
a function or derivative, or one step of an iterative process.
Robustness - How the correctness of the algorithm is affected by different types
of functions and different
types of inputs. For example, can an iterative method be relied on to find a
solution , even if
we start from a bad initial point?
Let’s use these criteria to compare and contrast the midpoint and rectangle
rules.
Cost Each algorithm performs a single function evaluation to estimate the
definite integral over a
subinterval, so the cost is identical. The total cost over the entire
computation grows linearly
with the number of intervals N in each case, meaning that there is some fixed
constant 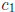 , not
, not
dependent on the number of intervals, such that the total cost is approximately
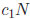 = O(N).
= O(N).
For example, if the number of intervals doubles, the cost of evaluating the
approximate integral
will double as well.
Speed Clearly as the size of each subinterval h gets smaller, the error gets
smaller as well. Is there
any difference between the speed with which the rectangle and midpoint rules
approach the
true solution, as h decreases (and the number of function evaluations
increases?)
Rectangle Rule -For the rectangle rule, the error approaches 0 in direct
proportion to the
rate at which h approaches 0. In other words, the error
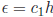 for some fixed
constant
for some fixed
constant
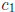 , or ε = O(h). For example, halving the size of h will halve the amount of
error.
, or ε = O(h). For example, halving the size of h will halve the amount of
error.
Midpoint Rule -For the midpoint rule, the error approaches 0 in proportion to
the rate at
which the square of h approaches 0. That is the error
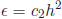 for some fixed
constant
for some fixed
constant
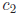 , or ε = O(h2). For example, halving the size of h will divide the error by 4.
This is a
, or ε = O(h2). For example, halving the size of h will divide the error by 4.
This is a
much faster rate of convergence in general.
Robustness For functions that are reasonably well-behaved, both methods are
quite robust. By
“well-behaved” we mean that the function f is not too “wiggly” relative to the
interval width
h. We make this concept more precise later.
Through this evaluation, we have shown that, in general, the midpoint rule is a
far better choice
than the rectangle rule for approximating the definite integral, since, for the
same cost, it will give
us a much more accurate answer.
5 Matlab
Matlab will be used for many of the assignments in this class. Many of you
already have experience
with it. There are a few ways to get up to speed:
• Links to some online resources are available from the course web site.
• A “Matlab Tutorial” is available from the DoIT Tech Store. A later version of
this same
document is the book Matlab Primer by K. Sigmon and T. A. Davis, 7th edition,
2004,
available from Amazon and elsewhere.
• The “help” command within Matlab itself is invaluable.
• Assignment 0 for this class has a brief introduction, as well as some
exercises to be handed
in.
| Prev | Next |