Introduction to Parametric Equations
Vickie Graziano
Introduction:
This lesson is designed for an Algebra II / Trigonometry class . It is a basic (no
trigonometry)
introduction to parametric equations. This lesson will be taught at the
conclusion of the unit on
systems of equations.
Objectives:
- The students will be introduced to the need for a parameter.
- The students will be able to write a set of parametric equations.
- The students will be able to graph basic parametric equations.
- The students will be able to eliminate the parameter to find a linear
equation .
Learning Activities
-Students will be given a problem (Question 1) that will require them to write
two functions in
terms of t and use those functions to answers questions regarding
location(Larson, Boswell,
Kanold, & Stiff, 2004). Students will be expected to work with others at their
table. This
question will be posted on Blackboard so that the students can explore the
question using their
tablet.
- The ideas that the students generate from this problem will be used to
introduce new
vocabulary.
- A new problem (Question 2) will be given where with teacher’s assistance
students will write a
set of parametric equations and use Geometer ’s Sketchpad to see the parametric
equations in
motion. The students will use this graph (see sketch here) and their prior
knowledge of graphs
to try to eliminate the parameter. Students will then graph their new linear
equation on
Geometer’s Sketchpad to see that the graphs are the same. (Murdock, Kamischke, &
Kamischke, 2004)
- Students will be asked to work in groups for a third problem (Question 3)
where they will
write a set of parametric equations, graph the equations and eliminate the
perimeter. The
groups will be asked to share their work and ideas with the whole class.
(Burger, et al., 2007).
Laptop Implications:
- The students will have access to all problems and Geometer’s Sketchpad files
through
Blackboard. The students will take notes and work on problems on their tablets.
Student work will be displayed while they are presenting their ideas .
Illinois Learning Standards:
- 8.A.4b Represent mathematical patterns and describe their properties using
variables and
mathematical symbols .
- 8.B.4a Represent algebraic concepts with physical materials, words, diagrams,
tables, graphs,
equations and inequalities and use appropriate technology.
- 8.B.5 Use functions including exponential , polynomial, rational, parametric,
logarithmic, and
trigonometric to describe numerical relationships .
Sources:
Burger, E., Chard, D., J, H. E., Kennedy, P. A., Leinwand, S. J., Renfro, F. L.,
et al. (2007). Algebra 2. Austin:
Holt, Rinehart and Winston.
Larson, R., Boswell, L., Kanold, T. D., & Stiff, L. (2004). Algebra II.
Evanston: McDougal Littell.
Murdock, J., Kamischke, E., & Kamischke, E. (2004). Discovering Advanced
Algebra. Emeryville: Key
Curriculum Press.
Question 1
Suppose an ant starts at one corner of a picnic tablecloth and moves in a
straight line, as
shown. The ant's position (x, y) relative to the edges of the tablecloth is
given for different
times t (in seconds)
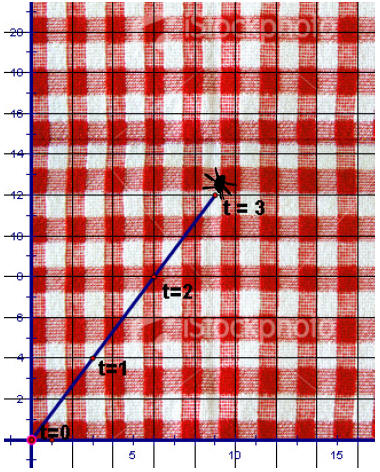
1. Write two equations: one that gives the ant's horizontal position x as a
function of t, and
one that gives the ant's vertical position y as a function of t.
2. What is the ant's position after 5 seconds
3. How long will it take the ant to reach an edge of the tablecloth?
Question 2
Hannah’s hot air balloon is ascending at a rate of 15 ft/s. A wind is blowing
continuously from
west to east at 24 ft/s. Write parametric equations to model this situation, and
decide whether
or not the hot-air balloon will clear power lines that are 300 feet to the east
and 95 feet tall.
Find the time it takes for the balloon to reach or pass over the power lines.
Question 3
As a cargo plane ascends after takeoff, its altitude increases at a rate of 40
ft/s. Its ground
distance from the airport increases at a rate of 240 ft/s.
a. Write equations for and draw a graph of the motion of the cargo plane. Then
find the
location of the cargo plane 20 second after takeoff.
b. Write an equation for the cargo plane’s altitude y in terms of ground
distance x.
| Prev | Next |