Lab on Linear and Quadratic Functions

Lab on Linear and Quadratic Functions
Handout for Teachers

Purpose: Gather some simple data and use it to model both linear and quadratic functions.

Audience: I did a version of this lab with Algebra Two students. As done, this lab uses an exact fit for the quadratic function and a regression fit for the linear data. At this point in the class we would have done both linear and quadratic functions. We do not talk about quadratic regression until pre-calculus, but it could be used for the points gathered, but I could not pass up the opportunity to teach systems of equations and matrices.

Procedure: With a digital camera that has a movie mode, take pictures of students shooting a basketball at the net. Give them three still frames and have them measure the height and distance the ball has traveled for the times stamped on the pictures. The students should then find a linear function for the horizontal distance that the ball has traveled and a quadratic function for the height. The students should write a paper that explains the process and results.

Specific Details:

1. With a digital camera on a tripod, place the camera far enough from the student shooting the basketball and the net so that you can see both in the frame. To make measuring distances a little easier, have the students stand directly in the middle (on a line between the two baskets ) of the court. Be sure the camera is near the middle of the line that is the perpendicular-bisector of the segment between the student and the net. Be sure there is some reference height in line with the student and net. You could use the rim of basket or another student.

2. Start taking the movie before the student shoots the ball and signal the student to shoot the ball at the basket while you are filming. My camera takes 6 frames per second, so I got movies that contained about 10 to 20 usable frames. (So if you wanted 15 ordered pairs for data analysis, you could make still pictures of each frame.) I am sure there must be some way to get coordinated on pictures more easily, but having the students use a ruler to measure and then ratios to convert to actual heights was enlightening.

3. Using a program like the Windows Movie Editor, capture three frames, one near the beginning, one near the middle, and one near the end of the flight. Windows Movie Editor shows you the elapsed time for each frame, from the time you started taking the movie. Look through the movie for the frame where the ball is just leaving the hand. Use this as time = 0.

4. I inserted the three still frames into a Word document and made the pictures as big as would fit on one sheet of paper. Give the students their own three pages, with the times indicated on each sheet for the frame.

5. The students will need to measure with a ruler the scaled height and distance that the ball has traveled and the scaled height (or length) of the reference. Using ratios, they can then convert everything to their favorite unit system. I let them use feet or meters.

6. Form two sets of ordered pairs, (time, horizontal distance) and (time, height) for the basketball. Using linear regression , find the function for the horizontal distance traveled as a function of time. Using the general quadratic function , y=at^2+bt+c , have the students plug in the information from the appropriate ordered pairs and use systems of equations (we used matrices to do this), find the values of a, b, and c.

7. Have the students write up a lab report which explains what they did. Things that I wanted to see in the lab report included:

 A. How they got the raw data they used and how they converted it to actual heights and distance.
 B. Show (with some explanation) the graphs of horizontal distance with respect to time, height with respect to time, and height w.r.t. distance.
 C. Have the students compare the values the got for a, b, and c in their quadratic function to the theoretical values. Of course, a should be one-half of the acceleration due to gravity and c should be the height from which the ball was released. Their value for b is the vertical component of the velocity, so that one is a little hard to explain to Algebra II students.
 D. Have the students predict whether or not the ball made it into (close to) the basket.
 E. If the coefficients they got were bad, or the shoot did not do what it was supposed to do, explain sources of error.

Basketball Lab

Purpose: The purpose of this lab is to toss a basketball in the direction of the basket and model both the horizontal distance and height of the ball with mathematical functions.

Procedure: A member of your “team” will toss a basketball from around the 3-point line at the basket. It will make measuring distances far easier if you are directly in the center (between the side lines) of the court in front of the basket. I will film your shooter taking the shoot and then provide you with three still frames. You will need to measure the distance the ball has traveled and the height of the ball using a ruler and then convert these measurements to actual distance and heights.

Report: You and your team members should gather the data, analyze it, and find two functions, both with time as the independent variable. One function will be for the distance the ball has traveled and one for the height of the ball. You should explain how you got these function. We will assume that the distance is a linear function and the height quadratic. For the purposes of this lab, we will ignore the influence of air resistance on the ball since it is very small. Once you have your functions and explained how you got them, you should plot these function first as functions of time, and then plot horizontal distance on the horizontal axis and height on the vertical axis to get a picture of the path of the ball. Use your calculations to predict if the ball will come anywhere close to the basket.

Be sure your report has a good introductory paragraph the engages the reader. Speaking of the reader, assume your reader knows as much algebra as you do but has not done a lab like this. Also include a conclusion that includes, among other things, how good you think you functions are. You may use the fact that for simple projectiles like this, the theoretical function for height is

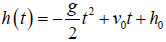
to compare your coefficients to the theoretical values. You can include screen shots from your calculator and can import the still frames into your document.

Grading: Your paper will be graded using the following:

 • Introduction: Does the opening paragraph introduce the reader to the lab? [10 pts]
 • Methods : Do you explain how the data was gathered and analyzed? Is all of the mathematics correct? [30 pts]
 • Relating Experimental Model to Theoretical Model: Have you related your model to the theoretical model for a projectile? [15 pts]
 • Conclusion: Do you summarize the results ? Have you included any sources of error? [10 pts]