MATH 1 - Sections 16 & 17 Handout for Chapter 5
MATH 1 - Sections 16 & 17 Handout for Chapter 5
Chapter 5 deals with Number Theory . Read page 221. We are
mainly
concerned with 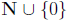 in this chapter. You should become conversant with
in this chapter. You should become conversant with
• b | a means b devides a,
• 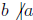 means b does not divide a
means b does not divide a
• factor, divisor, multiple , factorization (p.222), prime number , compos-
ite number, Sieve of Eratothenes (p.223-224)
• Divisibility tests (Table 2 on p.225), Definition of Theorem(p.225)
and the Fundamental Theorem of Arithmetic
• Obtaining the unique factorization by direct computation
• The theorem on the infinitude of primes
• The search for large primes, Mersenne numbers, GIMPS, Fermat Num-
bers, Euler formula, Escott formula
• HW 5.1: 1−24, Odd numbered exercises from 27 to 79, 80 and 81
• In section 5.2 we study about Perfect numbers , Deficient and Abundant
numbers, Amicable numbers, Weird and Dull numbers(?!), The man
who knew infinity, Definition of Conjecture(p.2, p.6), Goldbach's
conjecture, the Twin prime conjecture, Fermat's Last Theorem and
Andrew Wiles
• HW 5.2: 1−10, Odd numbered exercises from 11−43, 54, 56, 58-60.
• 5.3 treats the Greatest Common Factor (GCF), the Least CommonMul-
tiple( LCM ), Relatively prime numbers, Three methods for finding the
GCF and Three methods for finding the LCM
• HW 5.3: 1−10, 13, 15, 17, 21, 23, 25, 27, 33, 35, 37, 41, 43, 45, 47,
49, 50, 51, 55, 65, 67, 69.
• In 5.1 we discussed the formula for the number of all
divisors. If n =
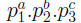 then N has (a+1)(b+1)(c+1) divisors. For example, in #59
then N has (a+1)(b+1)(c+1) divisors. For example, in #59
(p.232), 48 = 24.3 and so 48 has (4 + 1)(1 + 1) = (5) (2) = 10 divisors.
• #72, #73 (p.232): For n = 42  formula gives
(42)2 − (42) +
formula gives
(42)2 − (42) +
41 = 1763 = 43.41 which is composite. For n = 43 the formula gives
(43)2−(43)+41 = 1847 which can be verified to be a prime by checking
for prime factors below 43 since 43 is close to
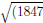 ).
).
• You have to study 5.2 carefully to understand proper divisors and find-
ing the sum of proper divisors. That can be used to classify every
number as perfect, abundant or deficient. Why are all prime numbers
deficient?
• 5.4 treats the well known Fibonacci Sequence
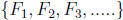 and the
and the
Golden Ratio
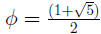 . HW for 5.4: 1-6, 15, 17, 20, 31.
. HW for 5.4: 1-6, 15, 17, 20, 31.
• We will briefly discuss Modern Cryptography (p.249 − 256) and Magic
Squares (p.265 − 270).
• As a review of your mastery of the concepts we discussed solve from
Chapter 5 test: 1-16, 18, 19.
• Using a program called Mathematica (created by Stephen Wolfram ) I
could establish that 5.7.11.13.17.19.23.29.31 = 33,426,748,355 is
an abundant number since the sum of its proper divisors is calculated
to be 33,459,293,245.
| Prev | Next |