Math 110 - Fall 05 - Lectures notes # 11

The next goal is to make explicit the connection between
matrices, familiar from Math 54, and linear transformations
T: V -> W between finite dimensional vectors spaces.
They are not quite the same, because the matrix that represents
T depends on the bases you choose to span V and W, and
the order of these bases:

Def: Let V be a finite dimensional vector space. An
ordered basis of V is a basis for V with an order:
{v_1,...,v_ n}, where n=dim (V).

Ex: Let e_ i = i- th standard basis vector (1 in i- th entry, 0 elsewhere)
Then the bases {e_1,e_2,e_3} and {e_2,e_3,e_1} are the same
(order in a set does not matter), but the ordered bases
{e_1,e_2,e_3} and {e_2,e_3,e_1} are different .

Def: For V = F^n, {e_1,...,e_ n} is the standard ordered basis.
For P_ n (F), {1,x,x^2,...,x_ n} is the standard ordered basis.

Given ordered bases for V and W, we can express both vectors
in V and W, and linear transformations T: V->W as vectors and
matrices with respect to these ordered bases:

Def: Let beta = {v_1,...,v_ n} be an ordered basis for V.
For any x in V, let x = sum_ {i=1 to n} a_ i*v_ i be the unique
linear combination representing x. The coordinate vector
of x relative to beta, denoted [x]_ beta, is

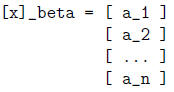
ASK & WAIT: What is [v_ i]_ beta ?
ASK & WAIT: Let V = P_5(F), beta = {1,x,x^2,x^3,x^4,x^5},
and v = 3-6x+x^3. What is [v]_ beta?
ASK & WAIT: If beta = {x^5, x^4, x^3, x^2, x, 1}?

Lemma: The mapping Beta: V -> F^n that maps x to [x]_ beta is linear.
Proof: if x = sum_ i a_ i*v_ i and y = sum_ i b_ i*v_ i, then
[x]_ beta = [a_1;...;a_ n], [y]_ beta=[b_1;...;b_ n] and

[x+y]_ beta = [sum_ i (a_ i+ b_ i)*v_ i]_ beta ... by def of x+ y
= [a_1+b_1 ; ... ; a_ n+ b_ n ] ... by def of []_beta
= [a_1 ; ... ; a_ n] + [b_1; ... ; b_ n]
= [x]_ beta + [y]_ beta ... by def of []_beta
Similarly, [c*x]_ beta = c*[x]_ beta

We need this representation of vectors in V as
coordinate vectors of scalars in order to apply T: V -> W
as multiplication by a matrix . We will also need to
represent vectors in W the same way.

Let beta = {v_1,...,v_ n} and gamma = {w_1,...,w_ m}
be ordered bases of V and W, resp. Let T: V -> W be linear.
Then there are unique scalars a_ {ij} such that
T (v_ j) = sum_ {i=1 to m} a_ {ij}*w_ i
These scalars will be the entries of the matrix representing T:

Def: Let T: V -> W be linear, V and W finite dimensional.
Using the above notation, the m x n matrix A with
entries a_ {ij}, is the matrix representation of T in the ordered
bases beta and gamma. We write A = [T]_ beta^gamma.
If V = W and beta = gamma, we write simply A = [T]_ beta

Note that column j of A is [a_{1j};...;a_ {mj] = [T (v_ j)]_ gamma

To see why we call A the matrix representation of T, let us use
it to compute y = T (x).

Suppose x = sum_ {j=1 to n} x_ j*v_ j, so [x]_ beta = [x_1;...;x_ n]
is the coordinate vector for x. We claim the coordinate
vector for y is just gotten by multiplying by A:
[y]_ gamma = A * [x]_ beta

To confirm this we compute:
y = T (x) = T (sum_ {j=1 to n} x_ j*v_ j) ... by def of x
= sum_ {j=1 to n} x_ j*T (v_ j) ... since T is linear
= sum_ {j=1 to n} x_ j*(sum_ {i=1 to m} a_ {ij}*w_ i)
... by def of T (v_ j)
= sum_ {j=1 to n} sum_ {i=1 to m} a_ {ij}*x_ j*w_ i
... move x_ j into sum
= sum_ {i=1 to m} sum_ {j=1 to n} a_ {ij}*x_ j*w_ i
... reverse order of sums
= sum_ {i=1 to m} w_ i * (sum_ {j=1 to n} a_ {ij}*x_ j)
... pull w_ i out of inner sum

so
[y]_ gamma = [ sum_ {j=1 to n} a_{1j}*x_ j ] = A * [ x_1 ] = A*[x]_ beta
[ sum_ {j=1 to n} a_{2j}*x_ j ] [ x_2 ] as desired
[ ... ] [ ... ]
[ sum_ {j=1 to n} a_ {mj}*x_ j ] [ x_ n ]

Ex: T: R^2 -> R^4, T((x, y) = (x-y, 3*x+2*y, -2*x, 7*y)
beta = standard basis for R^2, gamma = standard basis for R^4,
so T((1,0)) = (1;3;-2;0) and T((0,1)) = (-1;2;0;7), so
A = [ 1 -1 ] (for brevity in these notes, we will sometimes use
[ 3 2 ] "Matlab notation": T = [ 1 -1 ; 3 2 ; -2 0 ; 0 7 ] )
[-2 0 ]
[ 0 7 ]

ASK & WAIT: What if beta = {e2,e1} and gamma = {e3 e4 e1 e2}?

Suppose x = 3*e1 - e2; what is T (x)?
what is [T (x)]_ gamma, using standard bases?
T (x) = T(3,-1) = (4,7,-6,-7)
[T (x)]_ gamma = A * [3;-1] = [4;7;-6;-7]

Ex: T: P_3(R) -> P_2(R), T (f (x)) = f’ (x),
beta = {1, 1+x, x^2, x^3 }, gamma = {2 , x , x^2}
Then T(1) = 0, T(1+x) = 1 = (1/2)*2; T (x^2) = 2*x ; T (x^3) = 3*x^2
So T = [ 0 1/2 0 0 ]
[ 0 0 2 0 ]
[ 0 0 0 3 ]
ASK & WAIT: What is T if beta = { 1, x, x^2, x^3 }? If gamma={1,x,x^2}?

Having identified matrices with linear transformations between
two finite dimensional spaces with ordered bases, and recalling
that mxn matrices form a vector space, we will not be surprised
that all the linear transformations between any two vector
spaces is also a vector space:

Def: Let T and U be linear transformations from V -> W.
Then we define the new function T+ U: V -> W by (T+ U) (v) =T (v)+ U (v)
and the new function c*T: V -> W by (c*T) (v) = c*T (v)

Thm: Using this notation, we have that
(1) For all scalars c, c*T+ U is a linear transformation
(2) The set of all linear transformation from V -> W,
is itself a vector space, using
the above definitions of addition and multiplication by scalars

Proof:
(1) (c*T+ U) (sum_ i a_ i*v_ i)
= (c*T) (sum_ i a_ i*v_ i) + U (sum_ i a_ i*v_ i) ... by def of c*T+ U
= c*(T (sum_ i a_ i*v_ i)) + U (sum_ i a_ i*v_ i) ... by def of c*T
= c*(sum_ i a_ i*T (v_ i)) + sum_ i a_ i*U (v_ i) ... since T, U linear
= sum_ i a_ i*c*T (v_ i) + sum_ i a_ i*U (v_ i)
= sum_ i a_ i*(c*T (v_ i)+ U (v_ i))
= sum_ i a_ i*(c*T+ U) (v_ i) ... by def of c*T+ U
(2) We let T_0, defined by T_0(v) = 0_W for all v, be the
" zero vector " in L (V, W). It is easy to see that all the
axioms of a vector space are satisfied. (homework!)

Def: L (V, W) is the vector space of all linear transformations
from V -> W. If V=W, we write L (V) for short.

Given ordered bases for finite dimensional V and W, we get a
matrix [T]_ beta^gamma for every T in L (V, W). It is natural
to expect that the operations of adding vectors in L (V, W)
(adding linear transformations) should be the same as adding
their matrices, and that multiplying a vector in L (V, W) by a
scalar should be the same as multiplying its matrix by a scalar:

Thm: Let V and W be finite dimensional vectors spaces with
ordered bases beta and gamma, resp. Let T and U be in L (V, W).

Then
(1) [T+ U]_ beta^gamma = [T]_ beta^gamma + [U]_ beta^gamma
(2) [c*T]_ beta^gamma = c*[T]_ beta^gamma
In other words, the function []_beta^gamma: L (V, W) -> M_ {m x n} (F)
is a linear transformation.

Proof: (1) We compute column j of matrices on both sides
and comfirm they are the same. Let beta = {v_1,...,v_ n}
and gamma = {w_1,...,w_ m}. Then
(T+ U) (v_ j) = T (v_ j) + U (v_ j) so
[(T+ U) (v_ j)]_ gamma = [T (v_ j)]_ gamma + [U (v_ j)]_ gamma
by the above Lemma that shows the mapping x -> [x]_ gamma
was linear.
(2) Similarly (c*T) (v_ j) = c*T (v_ j) so
[(c*T) (v_ j)]_ gamma = [c*T (v_ j)]_ gamma
= c*[T (v_ j)]_ gamma by the Lemma
so the j-th columns of both matrices are the same

To summarize, what we have so far is this:
Given two ordered bases beta for V and gamma for W, we have
a one-to-one correspondence between
all linear transformations in L (V, W) and all matrices in M_ {m x n} (F).
Furthermore, this 1-to-1 correspondence " preserves " operations
in each set:
adding linear transformations <=> adding matrices
[ T + U <=> [T]_ beta^gamma + [U]_ beta^gamma ]
multiplying linear transformations by scalars
<=> multiplying matrices by scalars
[ c*T <=> c*[T]_ beta^gamma ]
applying linear transformation to a vector
<=> multiplying matrix times a vector
[ y = T (x) <=> [y]_ gamma = [T]_ beta^gamma * [x]_ beta ]

There are several other important properties of and operations
on linear transformations, and it is natural to ask what they
mean for matrices as well (we write A = [T]_ beta^gamma for short)
null space N (T) <=> set of vectors x such that A*x = 0
range space R (T) <=> all vectors of the form A*x
<=> all linear combinations of columns of A
T being one-to-one <=> Ax = 0 only if x=0
T being onto <=> span (columns of A) = F^m
T being invertible <=> A square and Ax =0 only if x=0

What about composition? If T: V -> W and U: W -> Z, then
consider UT: V -> Z, defined by UT (v) = U (T (v))

Thm: If T is in L (V, W) and U is in L (W, Z), then UT is in L (V, Z),
i.e. UT is linear.
Proof: UT( sum_ i a_ i*v_ i ) = U (T( sum_ i a_ i*v_ i )) ... by def of UT
= U( sum_ i a_ i*T (v_ i)) ... since T is linear
= sum_ i a_ i*U (T (v_ i)) ... since U is linear
= sum_ i a_ i*UT (v_ i) ... by def of UT

Thm:
(1) If T in L (V, W) and U1 and U2 are in L (W, Z), then
T(U1+U2) = TU1 + TU2 ( distributibity of addition over composition)
(2) If T in L (V, W), U in L (W, Z), and A in L (Z, Q), then
T (U A) = (T U) A is in L (V, Q) (associativity of composition)
(3) If T in L (V, W), I_ V the identity in L (V, V) and I_ W the identity in L (W, W),
then T I_ V = I_ W T = T (composition with identity)
(4) If T in L (V, W) and U in L (W, Z), and c a scalar, then
c (T U) = (c T) U = T (c U) (commutativity and associativity of
composition with scalar multiplication)
Proof: homework!

Now that we understand the properties of composition of linear transformations,
we can ask what operation on matrices it corresponds to:

Suppose T: V -> W and U: W -> Z are linear so UT: V -> Z
Let beta = {v_1,...,v_ n} be an ordered basis for V
gamma = {w_1,...,w_ m} be an ordered basis for W
delta = {z_1,...,z_ p} be an ordered basis for Z
with A = [U]_ gamma^delta the p x m matrix for U,
B = [T]_ beta^gamma the m x n matrix for T,
C = [UT]_ beta^delta the p x n matrix for UT
Our question is what is the relationship of C to A and B?
We compute C as follows:
column j of C = [UT (v_ j)]_ delta ... by def of C
= [U(T (v_ j))]_ delta ... by def of UT
= [U (sum_ {k=1 to m} B_ kj*w_ k)]_ delta ... by def of T (v_ j)
= [sum_ {k=1 to m} B_ kj*U (w_ k)]_ delta ... by linearity of U
= [sum_ {k=1 to m} B_ kj* sum_ {i=1 to p} A_ ik * z_ i]_ delta
... by def of U (w_ k)
= [sum_ {k=1 to m} sum_ {i=1 to p} A_ ik * B_ kj * z_ i]_ delta
... move B_ kj inside summation
= [sum_ {i=1 to p} sum_ {k=1 to m} A_ ik * B_ kj * z_ i]_ delta
... reverse order of summation
= [sum_ {i=1 to p} z_ i * (sum_ {k=1 to m} A_ ik * B_ kj)]_ delta
... pull z_ i out of inner summation
= [sum_ {k=1 to m} A_1k * B_ kj] ... by def of []_delta
[sum_ {k=1 to m} A_2k * B_ kj]
[ ... ]
[sum_ {k=1 to m} A_  mk * B_ kj]
said another way, C_ ij = sum_ {k=1 to m} A_ ik * B_ kj

Def: Given the p x m matrix A, and the m x n matrix B we define their
matrix-matrix product (or just product for short ) to be the p x n matrix C
with C_ ij = sum_ {k=1 to m} A_ ik * B_ k j

Thm: Using the above notation,
[UT]_ beta^delta = [U]_ gamma^delta * [T]_ beta^gamma

In other words, another correspondence between linear transformations
and matrices is:
composition of linear transformations <=> matrix-matrix multiplication