Math 1210-9 Exam #2 Review Questions
| These are some review questions for Exam #2. If
you can successfully complete these TYPES of questions, you should be well prepared for the exam . There is essentially one question per section to help you identify the key ideas on the exam. |
Chapter 2 (2.5 through 2.9)
1. Find the derivative of the following functions
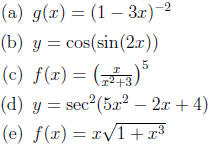
2. (a) Find 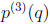 for
for
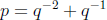
(b) Find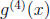 for
for
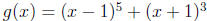
3. Use implicit differentiation to find
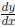
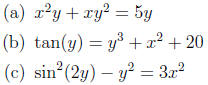
4. (a) A balloon is rising vertically at a rate of 2
ft/sec. An observer is located 300ft from
a point on the ground directly below the balloon. At what rate is the distance
between the balloon and the observer changing when the height of the balloon is
400 ft?
(b) The radius of a circle is increasing at the rate of 3 ft/sec. Find the rate
of change
of the area of the circle at the time that the radius is 15 ft.
(c) A conical tank has radius 3 ft and depth 10 ft. If water is poured into the
tankat
the rate of 2 cubic feet per minute, how fast is the water level rising when the
water
in the tank is 5 ft deep?
5. (a) Approximate 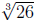 by using the differential
formula
by using the differential
formula 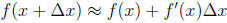 x.
x.
(b) Approximate 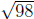 by using the differential
formula
by using the differential
formula
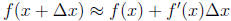 .
.
Chapter 3 (3.1 through 3.8, skip 3.7)
6. Use 3.1 methods to find the global min and global max of the following
functions:
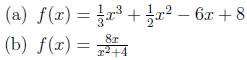
7. Consider 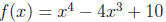
(a) Find all critical points for f(x)
(b) Determine where f(x) is increasing and decreasing.
(c) Find all local minimum and maximum locations AND values.
(d) Determine where f(x) is concave up and concave down.
(e) Find the x values of any inflection points.
(f) Use all of the above information to sketch a graph of f (x).
8. Repeat the previous question for the following functions:
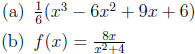
9. (a) Find two positive numbers whose sum is 17 and whose
product is a maximum .
(b) An open box is formed from a rectangular sheet of cardboard by cutting equal
squares from each corner and folding up the edges. If the dimensions of the
card-
board are 15 in by 24 in, what size squares should be cut to obtain a box of
maximum
volume? (see Ex 1 Section 3.4)
10. Consider 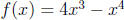 . Graph this fuction by
completing the following steps
. Graph this fuction by
completing the following steps
(a) Find the domain of the function
(b) Test for symmetry (is the function even, odd, or neither)
(c) Find the x and y intercepts of the function
(d) Find all critical points for the function
(e) Determine where the graph is increasing and decreasing
(f) Find all local minima and maxima
(g) Determine where the graph is concave up and concave down
(h) Identify any inflection points
(i) Find the asymptotes of the function (if applicable)
(j) Use all of this information to sketch a graph of the function
11. Repeat the previous question for
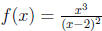
12. For each function below, decide whether the Mean Value Theorem applies on
the given
interval. If it does, find all possible values of c.
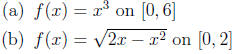
13. (a) Find 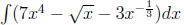
(b) Find 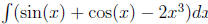
(c) (NEW!) Find 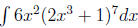
(d) (NEW!) Find 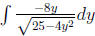
| Prev | Next |