Math 170 Exam
Math 170 Exam
PART I – Free response. Show all your work.
1. [5 points] Algebraically solve the equation 2x3 + 3x2
− 32x +15 = 0 . You may use rational zero test.
Solution : possible zeros are ±1, ± 3, ± 5, ±1/ 2, ± 3/ 2, ± 5 / 2
Use Synthetic division to find zeros . The zeros are –5, 3, 1/2
2. [5 points] Form a polynomial function g(x) with
real coefficients that has degree 4, leading coefficient 1, with zeros at 5
multiplicity 2, and −2i multiplicity 1.
Solution : f (x) = (x − 5) 2(x + 2i)(x − 2i) = x 4−10x
3+ 29x 2− 40x +100
4. [5 points] Find the accumulated value of an
investment of $12,000 at rate of interest of 7.5% compounded monthly for 15
years. Round your answer to the nearest cent
Solution: A =12000(1+ 0.075/12) 12 × 15 36833.42
5. [5 points] What initial investment at 5 %
interest compounded continuously for 6 years will accumulate to $75,000? Round
your answer to the nearest cent.
Solution: 75000 p(e 0.05 ×6) ⇒p =55561.37
6. [5 points] Use the properties of logarithms to
expand the logarithmic expression as much as possible.
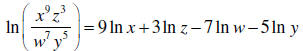
7. [5 points] Use the properties of logarithms to
condense the logarithmic expression as much as possible. Be sure to simplify.
,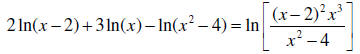
8. [5 points each] Algebraically solve the
following equations for x .
a.
62x-5=36
2x-5=2
x=3.5
b.
e2x-5ex+4=0
ex=1⇒ x=0,ex=4 ⇒x=ln4
9. The formula A = (15.9)e 0.0235 tmodels
the population of Florida, A , in millions, t years after 2000.
a. [4 points] What was the population of Florida in 2000?
Answer: A0 =15.9 million
b. [4 points] When will the population of Florida reach 19.2 million?
Answer: In 2008
10. [5 points] Form a rational function f (x) with
the following characteristics:
1. Vertical asymptotes at x = 4 and x = −6
2. Horizontal asymptote at y = 0
3. x - intercepts at x = −5 and x = 7
Answer: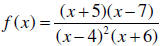
PART II – Multiple choice . Chose the response that best
completes the statements or answers the question. Write the
letter on the blank line . Use capital block letters A, B, C, D, E. Each problem
is worth 5 points.
_______1. Use the leading coefficient test to determine the end behavior of the
polynomial function
g(x) = −4(x + 2)(x − 5)6
A. rises to the left and falls to the right
B. rises to the left and rises to the right
C. falls to the left and falls to the right
D. falls to the left and rises to the right
E. None of these.
_______2. Find the domain of the logarithmic function f (x) = ln(3x − 21)
A. (4,∞)
B. (7,∞)
C. (− ∞,4)
D. (− ∞,7)
E. None of these
_______3. Write the equation in its equivalent exponential
form: log 7(x − 2) = y .
A. ( x −2) 7= y
B. 7x−2=y
C. 7 y= x − 2
D. y7 = x − 2
E. None of these
_______4. Write the equation in its equivalent logarithmic
form : ex= y + 8
A. ln(y + 8) = x
B. log(y + 8) = x
C. ln(x) = y + 8
D. log(x) = y + 8
E. None of these.
_______5. Find the equation(s) of the vertical asymptote(s),
if any, of the graph of the rational function
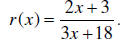
A.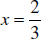
B. x = −6
C. x = 0
D. x = 6
E. None of these.
_______6. Divide 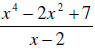 .
.
A.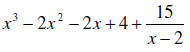
B.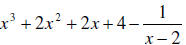
C.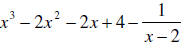
D.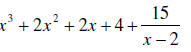
_______7. The rational function 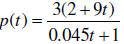 models
the population of deer that live in Pokagon State Park., where t is
models
the population of deer that live in Pokagon State Park., where t is
measured in years. According to the model, what happens to the Pokagon deer
population in the long run?
A. The population levels off to 200
B. The population levels off to 400
C. The population levels off to 600 D. The population grows to infinitely large
E. None of these.
_______8. Determine the x-intercept for the function f (x)
= log(3x − 8) − 2.
A.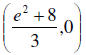
B. (36,0)
C. (3,0)
D.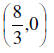
E. None of these.
_______9. What is the multiplicity of the x = 2 zero for
the function g(x)=8x3(x-2)5(x+3)4?
A. 2 B. 3 C. 4 D. 5 E. None of these.
______10. If the half-life of a radioactive element X is 6
seconds, with 128 grams of X initially,
after 12 seconds, how many grams of X are present ?
A. 64 grams B. 32 grams C. 16 grams D. 8 grams E. None of these.
| Prev | Next |