Math 223b Homework 2 Solutions
HW2 Solutions
Let’s do the short answer questions first...
Problem 2
1. Camera Baseline (3 pts): Assume you want to use two of the webcams from last
week's assignment
for stereo. Your project requirements state that you should be able to
distinguish a point that is 10m
from your camera from one 9m away. How far away do you have to place your two
cameras
horizontally if you want their viewing directions to be parallel?
This problem presents the complication that it’s not entirely possible to
predict how a continuous
disparity will translate into a discrete disparity without more information...
so we’ll accept multiple
solutions to this problem :
Solution 1
Another approach is to assume that the disparity between the 9m object and the
10m object will be
exactly one pixel. In other words:
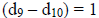
...using the formula from the text and substituting for disparities :
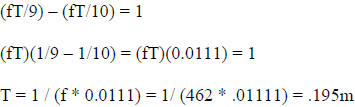
The catch with this solution is that if I plug back in to get the actual
disparities, I see that:
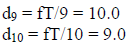
So the disparities are indeed different by one pixel ... but I know that given a
real system computing
real disparities , there is some point where I could get d9 equal to one and d10
equal to zero, if you
imagine just gradually widening the baseline from 0 until the disparity of the
9m object popped from
zero to one .
So this is the “conservative” solution...
Solution 2
A good trick here is to assume that the 9m object will be the farthest possible
object that just barely gives us one
pixel of disparity. This lets me avoid doing any computation with the 10m
object… the important thing is that
decreasing the baseline decreases disparity, so if I do find the baseline that
just barely gives me exactly one pixel
of disparity at 9m, I know that I have the smallest acceptable baseline. And by
definition I’ll have zero pixels of
disparity at 10m (or 9.00001m, for that matter), so I know I can distinguish the
9m object from the 10m object.
Now page 144 in the book tells us the relationship between depth and disparity:
Z = f * (T/d)
...where Z is object distance, f is camera focal length, T is the baseline, and
d is the observed disparity.
I want a disparity of 1 pixel (i.e. 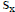 ) at a Z
(distance from the camera plane) of 9m, and f/
) at a Z
(distance from the camera plane) of 9m, and f/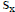 is 462 (from your
is 462 (from your
first homework, or from the assignment FAQ). Doing the substitutions , I get:
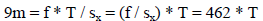
…and solving for T , I get 0.0195m.
Note that if I made T any smaller, I would need a larger depth to make d =
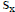 , so I wouldn’t be able to tell the
, so I wouldn’t be able to tell the
9m object from the 10m object. So this really is the smallest acceptable
baseline…
The catch with this solution is that this basically assumes that disparities are
continuous (which is an aggressive
assumption, but you have no information to the contrary), or that I can estimate
disparities with fantastic
subpixel accuracy.
2. Depth recovery (2 pts): Can depth be recovered from a stereo pair taken under
the following
circumstances? Briefly justify your answers.
(a) Two images taken by orthographic projection from cameras with parallel
optical axes?
No. An orthographic camera only captures rays that are parallel to its optical
axis, so none of the rays
captured by the two cameras could possibly intersect, making depth triangulation
impossible.
(b) Two images taken by a single perspective proj. camera rotated about its
optical center?
No. Capturing two images from the same location at two orientations is
equivalent to having a stereo
rig with a baseline of zero; triangulating depth is impossible in this
configuration.
Matlab Solutions
A simple solution is presented as ‘stereo.m’, along with a tester program called
‘test_stereo.m’.
An optimized solution that uses convolution to replace loops, performs more
extensive
precomputation , and performs left-right consistency checking is presented as ‘stereoOpt.m’,
along with
a tester program called ‘test_stereoOpt.m’. The original m-files are available
on the course web page
at cs223b.stanford.edu.
| Prev | Next |