Math 3B Final Exam Review
The problems on the final will be similar to the ones from
the homework assignments,
quizzes and midterms. The exam will be about twice as long as the midterms and
will
emphasize the newer material covered since the last midterm (sections 6.1-6.5,
8.1-8.3).
However, it will be cumulative and may include questions on any of the material
covered
this quarter (sections 4.10, 5.1 - 5.5, 7.1-7.5, 7.8). Also, be advised that to
do many of the
problems on the new material, you will need to evaluate integrals and that
requires knowledge
of integration techniques, etc. Below is an outline of the different topics you
should know,
along with lists of practice problems from Stewart. This list is not exhaustive:
only the
most important topics from earlier sections have been included. The midterm
review sheets
provide information on additional topics .
1. Areas of Regions (6.1, 5.2). Calculate the area between two curves y =
f(x) and
y = g(x). Often this requires finding where the graphs intersect by solving f(x)
= g(x)
for x. But be careful, drawing an acurate picture of the region can be crucial.
(6.1 #
9, 13)
2. Volumes of Revolution. If R is a region in the xy-plane, calculate the
volume of
the solid obtained when R is rotated about one of the axes or a line parallel to
one of
the axes. (6.2 # 3, 9, 25, 27, 29, 31, 35, 6.3 # 5, 9, 19)
(a) Disk Method (6.2). 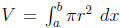 . Use this
method when R is the region
. Use this
method when R is the region
under the graph of y = f(x), and it is being rotated about a HORIZONTAL line.
If the axis of revolution is y = c, then r = f(x) - c.
(b) Washer Method (6.2). 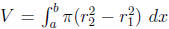 . Use this
when R is the region
. Use this
when R is the region
between two curves y = f(x) and y = g(x) for a ≤ x ≤ b, and it is
rotated about
a HORIZONTAL line. If y = c is the axis of revolution, then
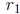 = f(x) - c and
= f(x) - c and
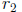 = g(x) - c.
= g(x) - c.
(c) Cylindrical Shells (6.3). 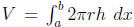 . Use
this method when R is the
. Use
this method when R is the
region between two curves y = f(x) and y = g(x) for a ≤ x ≤ b, and
it is rotated
about a VERTICAL line. If x = c is the axis of revolution, then r = x - c and
h = f(x) - g(x).
(d) NOTE: If the region is between two curves with equations x = f(y) and
x = g(y),
then you should integrate with respect to y. In this case, if the axis of
revolution
is Vertical, use Washers or Disks. If it is horizontal, use Cylindrical Shells.
3. Work (6.4). Calculate the work done moving an object with a variable
force F(x)
from x = a to x = b. You may also need to find an equation for F(x) from a word
problem. ((6.4 # 15, 29))
4. Average Value (6.5). Calculate the average value of a function f(x) on
an interval
[a, b]. (7.1 # 59)
5. Arclength (8.1). Calculate (or at least set up
an integral for) the arclength of a
segment of a curve y = f(x) (or x = g(y)). (8.1 # 9, 11, 19)
6. Surface Area (8.2). Calculate (or at least set up integrals for) the
surface area of
the surface obtained by rotating a curve y = f(x) about the x- or y-axis. (8.2
# 3, 5,
11, 26)
7. Hydrostatic Force (8.3). Compute the hydrostatic force on the side of
an object
submerged in a liquid. (8.3 # 11, 15)
Earlier Topics
8. Integration Techniques (7.1-7.5). Section 7.5 gives a good overview of
integration
strategies.
(a) Integration Formulas . Review the table on p. 506. You need to know
numbers
1-10, 11, and 13; while 12, 14, 17 and 18 are also useful.
(b) Substitution (5.5). Remember the two guidelines for choosing u:
1) u should correspond to the “inside” function in a composition; and
2) du = u'(x) dx should appear in the integrand, or at least be expressible in
terms of u .
DON’T FORGET to either change the limits of integration OR convert the
antiderivative
back into terms of x. (5.5 23, 43, 61, 7.5 # 5, 19 )
(c) Integration by Parts (7.1). Know when to use integration by parts,
and how
to choose u and dv (eg., u = L.I.A.T.E.). Be aware that some problems require
two applications of integration by parts, or some combination of u -substitution
and integration by parts. (7.1 # 7, 23, 25, 29, 31, 35)
(d) Trigonometric Integrals (7.2). Be able to integrate
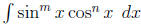 and
and
simple variations (like replacing the x’s with (3x) or when m = 3 and n = 1/2.)
(7.2 # 1, 5, 9, 15)
(e) Trigonometric Substitution (7.3). Know when to make the substitution
x =
a sinθ to simplify an integral, and how to convert the antiderivative back
into
terms of x by drawing a right triangle. (7.3 # 7, 11, 29 (do u-sub.
first))
(f) Integrating Rational Functions (7.4). Know how to use long division
of
polynomials and the method of partial fractions to algebraically simplify
rational
functions, so that they can be integrated easily. (7.4 # 8, 10, 13, 47)
9. Improper Integrals (7.8). Be able to recognize an improper integral.
In particular,
when you see any definite integral 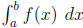 , you
should check to see if f(x) has a
, you
should check to see if f(x) has a
vertical asymptote between a and b. More importantly, you should be able to
evaluate
an improper integral USING LIMITS. (7.8 # 9, 13, 15, 27, 33)
10. Comparison Theorem (7.8). Determine whether an
improper integral converges or
diverges by using the Comparison Theorem. (7.8 # 49. 51, 53)
11. Given a graph of a function f(x), you should be able to sketch a graph of an
antiderivative
of f(x). If the antiderivative is defined by an integral, eg.
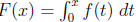 , then
, then
you should be able to compute values of F (x) by interpreting the integral as a
“net
area”. (4.10 #47; 5.3 # 3.)
12. You should be able to write an area or a definite integral as a limit of
Riemann sums,
and interpret a limit of Riemann sums as a definite integral. ( 5.1 # 19;
5.2 # 17, 19,
29)
13. You should know what the Fundamental Theorem of Calculus, Parts I and II,
say and
how to use them to (1) find the derivative of a function defined as an integral,
and (2)
evaluate a definite integral. (5.3 # 11, 49, 55)
| Prev | Next |