Matrices and Vectors
3 Matrices and Vectors
This Section is a very concise introduction to the algebra of matrices and
vectors. This will let us
study mathematical models of the types we saw in the preceding illustrative
examples in a more
general, unified fashion.
3.1 Matrices
A (real) matrix of size m *n is an array of mn real numbers arranged in m rows
and n columns:

The n*m matrix AT obtained by exchanging rows
and columns of A is called the transpose of
A. A matrix A is said to be symmetric if A = AT .
The sum of two matrices of equal size is the matrix of the entry-by-entry sums,
and the scalar
product of a real number a and an m *n matrix A is the m* n matrix of all the
entries of A, each
multiplied by a . The difference of two matrices of equal size A and B is
A - B = A + (-1)B :
The product of an m *p matrix A and a p* n matrix B is an m* n matrix C with
entries
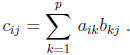
Examples
Let 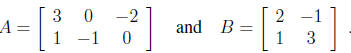
Then,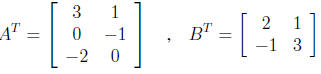
and
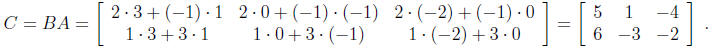
The product AB is not defined, because A and B have incompatible sizes. Furthermore,
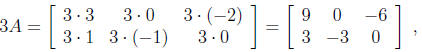
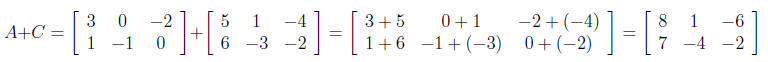
and
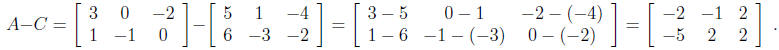
3.2 Vectors
A (real) n-dimensional vector is an n-tuple of real numbers
v = (v1,..., vn) .
There is a natural, one-to-one correspondence between n-dimensional vectors and
n *1 matrices:
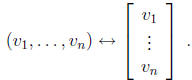
The matrix on the right is called the column vector
corresponding to the vector on the left.
There is also a natural, one-to-one correspondence between n-dimensional vectors
and 1* n
matrices:
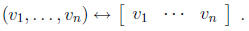
The matrix on the right is called the row vector corresponding to the vector on
the left.
If a is a vector, then the symbol a also denotes the corresponding column
vector, so that the
corresponding row vector is aT .
All algebraic operations on vectors are inherited from the corresponding matrix
operations,
when defined. In addition , the inner product of two n-dimensional vectors
a = (a1,..., an) and b = (b1,..., bn)
is the real number equal to the matrix product aTb. It is easy to
verify that this is also equal to
bT a. Two vectors that have a zero inner product are said to be
orthogonal.
The norm of a vector a is
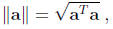
obviously a nonnegative number . A unit vector is a vector
with norm one.
Examples
The vector a = (2, -1, 0) corresponds to row vector aT = [2, -1, 0]
and to column vector
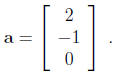
3.2 Vectors
The inner product of a and b = (1, 0, -1) is
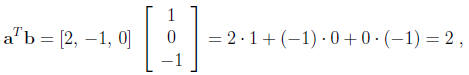
and the norm of a is
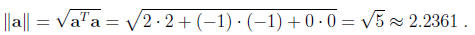
The vector
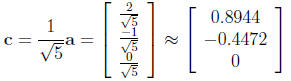
has unit norm:
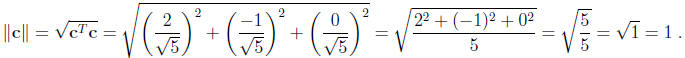
| Prev | Next |