Matrix Operations
Warm-up
1. Identify the rows and columns in the array of numbers.
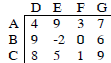
Rows : A, B, C
Columns: D, E, F, G
2. In the above array of numbers, what number is in the second row, third
column?
0
3. Write 4% as a decimal .
.04
4. What is 100 increased by 4% of 100?
104
5. Find this product : 1.04 ·100.
104
6. Suppose you want to increase a number by 6%. How can you do this using one
operation ?
Multiply by 1.06
Section 3-5 Matrix Operations
Matrix: An arrangement of numbers in rows and columns. Plural is matrices.
Elements of a matrix: The numbers in the matrix.
Example: The element is Row 2 Column 3 is 0.
Dimensions of a matrix: Number of rows by the number of columns.
Example: 3 x 4 are the dimensions of the matrix in the warm-up.
Example 1: What is the dimension of the matrix
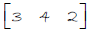
Solution : 1 x 3
Rows x Columns
Scalar multiplication: Multiplying a matrix by a number. Each element in the
matrix is
multiplied by that number .
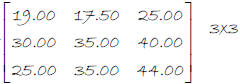
Example 2: The table shows the prices of each item.
| Shirts | Jeans | Sweaters | |
| Kids’ | 19.00 | 17.50 | 25.00 |
| Women’s | 30.00 | 35.00 | 40.00 |
| Men’s | 25.00 | 35.00 | 44.00 |
a. Arrange this data in a matrix. What are the dimensions?
b. The store is giving 25% off on all items. Use scalar multiplication to find
the
matrix of sale prices.
c. In the new matrix, where can you find the sale price for women’s sweaters?
Solution :
a.
| Shirts | Jeans | Sweaters | |
| Kids’ |
 |
||
| Women’s | |||
| Men’s | |||
b. 25% off. The customer will pay 75% off the original price. Multiply the
matrix
by 75%.
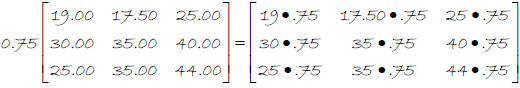
| Shirts | Jeans | Sweaters | ||
| Kids’ |
 |
|||
| = | Women’s | |||
| Men’s | ||||
c. The sale price for women’s sweaters is the second row, third column, $30
Matrix Addition and Subtraction
When two matrices have the same dimensions, you can add or subtract the matrices
by
adding or subtracting the elements in corresponding positions.
Example 3: Use the matrices 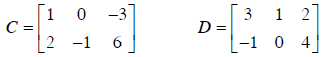
a. Find C + D
b. Find 2C – D
Solution : C is 2 x 3 and D is 2 x 3 so the matrices can be added or subtracted.
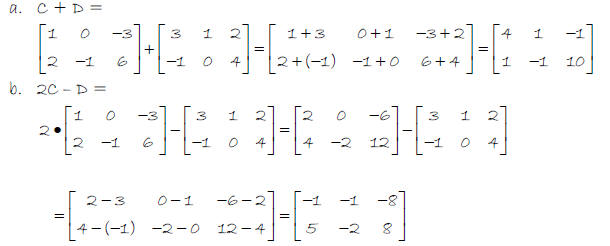
Why can’t you add or subtract matrices with different
dimensions ?
Because they don’t have the same number of elements.
| Prev | Next |