Multiplying Polynomials
We have seen that adding or subtracting algebraic terms is
limited to like terms
and multiplication can be done to any terms.
Exponential Expressions :
We have been using natural number exponents to indicate repeated
multiplication.
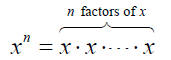
We have several important laws to follow when multiplying:

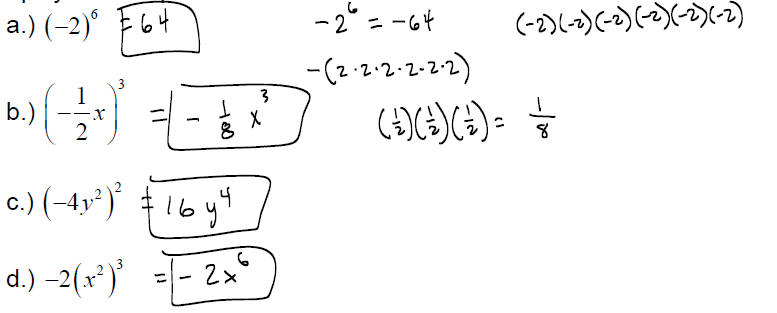
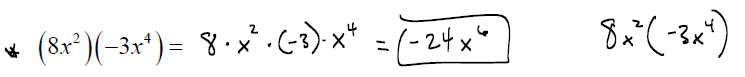
Multiplying a Polynomial by a Monomial :
To multiply a monomial and a polynomial , we use the distributive property.
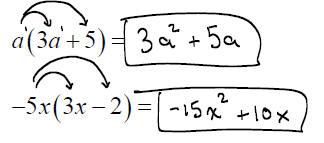
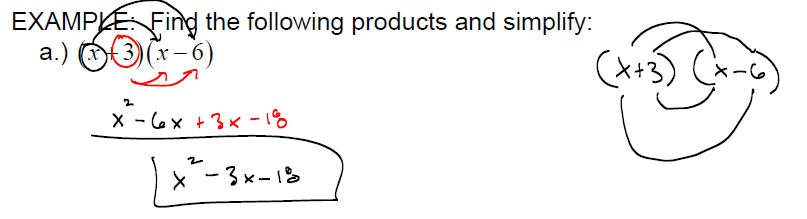
EXAMPLE: Find the following products:
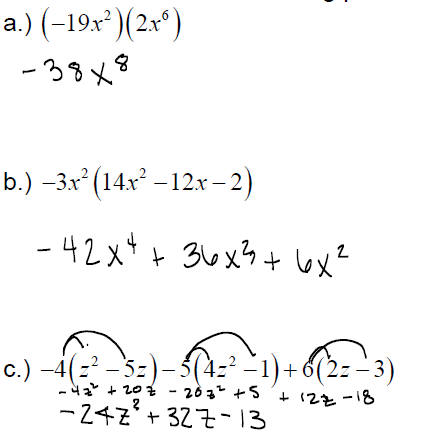
Multiplying a Polynomial by a Binomial :
To multiply a polynomial and a binomial, we use the distributive property
more than once.
Consider multiplying: (2a − 4)(3a + 5)
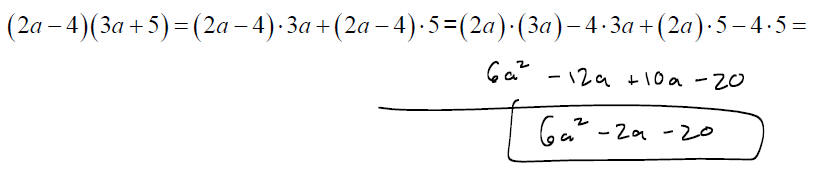
To multiply two binomials , multiply each term in the first
binomial by each
term in the second binomial.
The FOIL Method
When we have the product of two binomials, the above procedure tells us
we can:
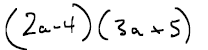
1.) Multiply the First terms: 2a and 3a to obtain 6a2 .
2.) Multiply the Outer terms: 2a and 5 to obtain 10a
3.) Multiply the Inner terms: −4 and 3a to obtain −12a
4.) Multiply the Last terms: −4 and 5 to obtain −20
Then simplify the resulting polynomial if possible:
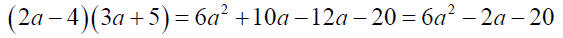
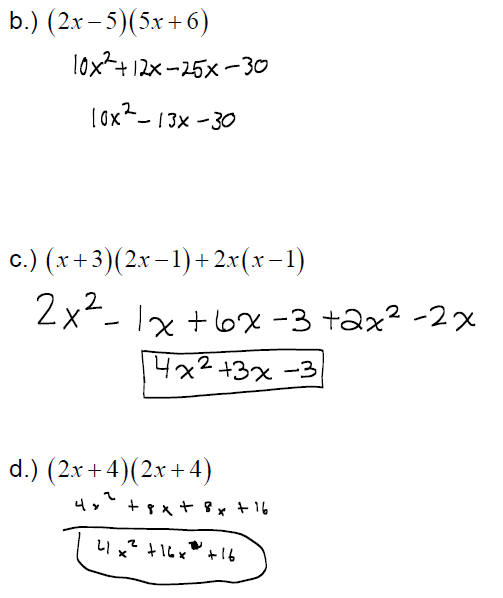
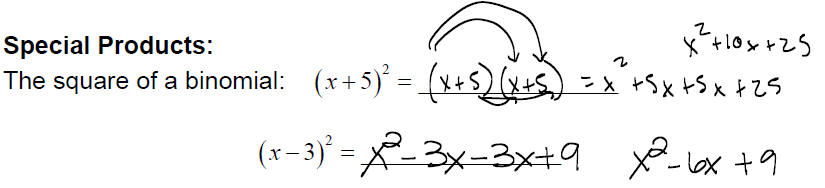
The product of the sum and difference of two terms :
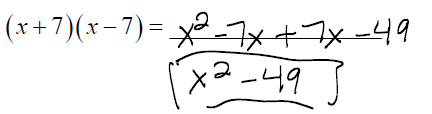
Multiplying Polynomials:
To multiply one polynomial by another, multiply each term of one polynomial
by each term of the other polynomial.

APPLICATION PROBLEMS
If two less than a certain number is multiplied by three more than the number,
the product is one less than the square of the number . Find the number.
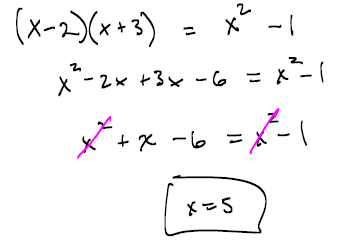
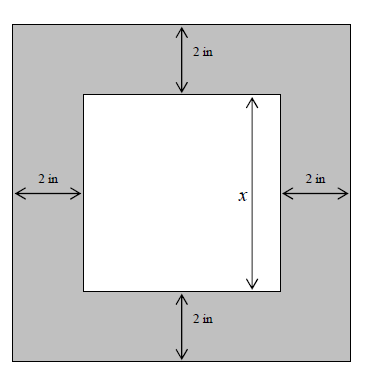
A square picture is surrounded by a frame that uniformly
measures 2 inches
wide. If the area of the
frame is 48 square inches, find the dimensions of the picture.
(Hint: The area of the whole thing equals the area of the
picture plus the
area of the frame.)
| Prev | Next |