One Sided Limits and Limits at Infinity
Example (Finding Horizontal Asymptotes) Find the horizontal asymptote of the
graph of the function
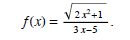
Solution . Dividing both numerator and denominator by x and using the properties
of limits, we have
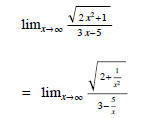
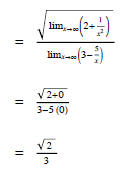
Therefore, the line
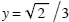 is a horizontal asymptote. It is also important to
realize that
is a horizontal asymptote. It is also important to
realize that
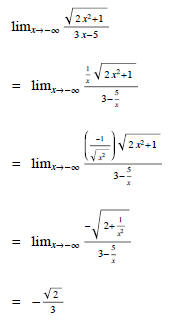
Therefore, the line
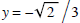 is another horizontal asymptote.
is another horizontal asymptote.
Example (Finding Horizontal Asymptotes) Find the horizontal asymptote of the
graph of the function
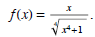
Solution . Dividing both numerator and denominator by x and using the properties
of limits, we have
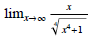
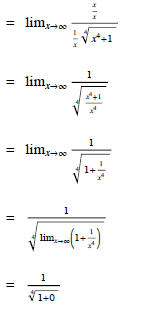
Therefore, the line y = 1 is a horizontal asymptote. In computing the limit x→ -∞
we must remember that for x < 0, we
have
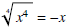 , so when we divide the numerator by x , when x < 0 we have,
, so when we divide the numerator by x , when x < 0 we have,
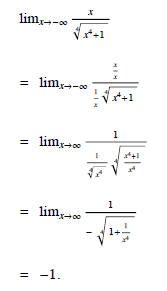
Therefore, the horizontal asymptotes are y = ± 1.
Exercises
(1) Sketch the graph of the function
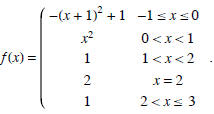
and then use the graph to determine which the following statements about the
function y = f(x) are true and which are
false?
(a) lim→0+ f (x) = 1
(b) limx→2 f (x) does not exist
(c) limx→2 f (x) = 2
(d) limx→1- f (x) = 2
(e) limx→1+ f (x) = 1
(f) limx→1 f (x) does not exist
(g) limx→0+ f (x) = limx→0- f (x)
(h) limx→c f (x) exists at every c in the open interval (-1, 1).
(i) limx→c f (x) exists at every c in the open interval (1, 3).
(j) limx→0- f (x) = 0
(k) limx→3+ f (x) does not exist
(2) Sketch the graph of the function
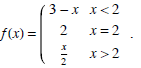
and then use the graph to determine the following?
(a) Find limx→2+ f (x), limx→2- f (x), and f (2).
(b) Does limx→2 f (x) exist? If so, what is it? If not, why not?
(c) Find limx→-1- f (x) and limx→-1+ f (x).
(d) Does limx→-1 f (x) exist? If so, what is it? If not, why not?
(3) Let 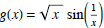 Use the graph of g to determine the following,
Use the graph of g to determine the following,
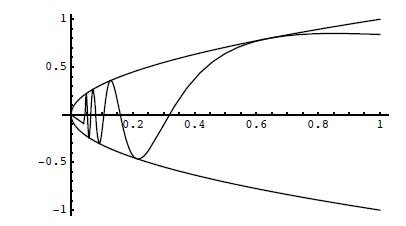
(a) Does limx→0+ g(x) exist? If so, what is it? If not, why not?
(b) Does limx→0- g(x) exist? If so, what is it? If not, why not?
(c) Does limx→0 g(x) exist? If so, what is it? If not, why not?
(4) Graph 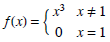 .Find limx→1- f (x) and limx→1+ f (x). Does limx→1 f (x) exist? If so, what is
it? If not, why
.Find limx→1- f (x) and limx→1+ f (x). Does limx→1 f (x) exist? If so, what is
it? If not, why
not?
(5) Graph 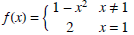 . Find limx→1- f (x) and limx→1+ f (x). Does limx→1 f (x) exist? If so, what is
it? If not,
. Find limx→1- f (x) and limx→1+ f (x). Does limx→1 f (x) exist? If so, what is
it? If not,
why not?
(6) Graph 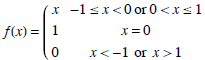 .
.
(a) What is the domain and range of f ?
(b) At what points c, if any does limx→c f (x) exist?
(c) At what points does only the left-hand limit exist?
(d) At what points does only the right-hand limit exist?
(7) Find the one-sided limit algebraically ,
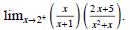
(8) Find the one-sided limit algebraically ,
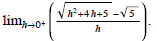
(9) Find the one-sided limit algebraically ,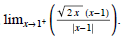
(10) Find the two -sided limit,
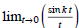 where k is a constant.
where k is a constant.
(11) Find the two -sided limit,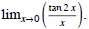
(12) Find the two -sided limit,
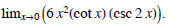
(13) Find the two-sided limit,
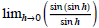 .
.
(14) Find the two-sided limit,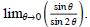
(15) Find the limit of the function
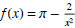 as x→+∞ and x→-∞.
as x→+∞ and x→-∞.
(16) Find the limit of the function
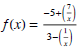 as x→+∞ and x→-∞.
as x→+∞ and x→-∞.
(17) Find the limit of the function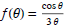 as
θ →+∞ and θ →-∞.
as
θ →+∞ and θ →-∞.
(18) Find the limit of the function
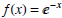 sin x as x→+∞ and x→-∞.
sin x as x→+∞ and x→-∞.
(19) Find the limit of the function
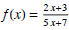 as x→+∞ and x→-∞.
as x→+∞ and x→-∞.
(20) Find the limit of the function
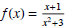 as x→+∞ and x→-∞.
as x→+∞ and x→-∞.
(21) Find the limit of the function
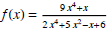 as x→+∞ and x→-∞.
as x→+∞ and x→-∞.
(22) Find the limit of the function
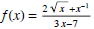 as x→+∞ and x→-∞.
as x→+∞ and x→-∞.
(23) Find the limit of the function
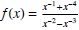 as x→+∞ and x→-∞.
as x→+∞ and x→-∞.
| Prev | Next |