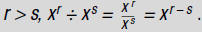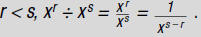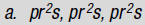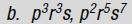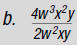POLYNOMIAL OPERATIONS
POLYNOMIAL OPERATIONS
| Here's what you'll learn in this lesson: Adding and Subtracting a. Definition of polynomial, term, and coefficient b. Evaluating a polynomial c. The degree of a term and a polynomial d. Writing the terms of a polynomial in descending order e. Definition of a monomial, binomial, and trinomial f. Recognizing like or similar terms g. Combining like or similar terms h. Polynomial addition i. Polynomial subtraction Multiplying and Dividing a. Multiplying a monomial by a monomial b. Multiplying a monomial by a polynomial c. Dividing a monomial by a monomial d. Dividing a polynomial by a monomial |
OVERVIEW
Every day, people use algebra to find unknown quantities.
For example, you may be
interested in figuring out how long it would take you to drive across the
country. Or, you
may want to know why your checkbook doesn't balance.
To find these unknown quantities, you need to be able to add, subtract,
multiply, and
divide polynomials. That’s what you will learn in this lesson.
EXPLAIN
ADDING AND SUBTRACTING
Summary
Identifying Polynomials
A polynomial is a special kind of algebraic expression
which may have one or more
variables and one or more terms .
For a polynomial in one variable, x, each term has the form axr,
where the coefficient, a,
is any real number , and the exponent, r, is a nonnegative integer.
For example:
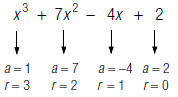
For a polynomial in two variables , x and y, each term has
the form axrys, where a is any
real number , and r and s are nonnegative integers.
For example:
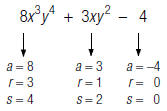
Polynomials with one, two, or three terms have special names:
A monomial has one term: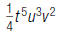
A binomial has two terms: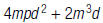
A trinomial has three terms: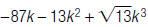
An algebraic expression is not a polynomial if any of its
terms cannot be written in the
form axr.
For example, these algebraic expressions are not polynomials:
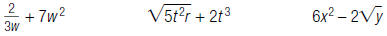
| Remember, when x≠ 0: x 0= 1 x 1 = x |
The Degree of a Polynomial
The degree of a term of a polynomial is the sum of the exponents of the
variables in that
term. The degree of a polynomial is the degree of the term with the highest
degree.
For example, to find the degree of the polynomial
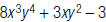 ; find the degree of
; find the degree of
each term:
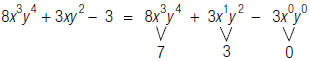
The degree of the polynomial
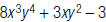 is the degree of the term with the
is the degree of the term with the
highest degree, 7.
Evaluating Polynomials
Sometimes the variables in a polynomial are assigned specific numerical values .
In these
cases you can evaluate the polynomial by replacing the variables with the
numbers.
To evaluate a polynomial:
1. Replace each variable with its assigned value.
2. Calculate the value of the polynomial .
For example, to evaluate the polynomial 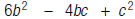 when
b = 2 and c = 3:
when
b = 2 and c = 3:
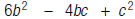 |
|
| 1. Replace b with 2 and c with 3. | 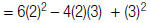 |
| 2. Calculate. | 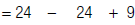 |
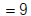 |
So, when b = 2 and c = 3, 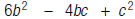 =9.
=9.
Adding Polynomials
To add polynomials, combine like terms - terms that have the same variables with
the
same exponents.
Here is an example of two like terms:
3x2y and –2x2y
Here is an example of two terms that are
not like terms:
3x2y and 3xy2
To add polynomials:
1. Remove the parentheses .
2. Write like terms next to each other.
3. Combine like terms.
| For example, to find: | 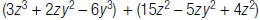 |
| 1. Remove the parentheses. | 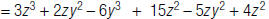 |
| 2. Write like terms next to each other. | 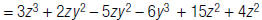 |
| 3. Combine like terms. | 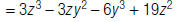 |
Subtracting Polynomials
To subtract one polynomial from another, add the opposite of the polynomial
being subtracted.
To subtract polynomials:
1. Multiply the polynomial being subtracted by –1.
2. Distribute the –1.
3. Simplify.
4. Write like terms next to each other.
5. Combine like terms.
For example, to find:
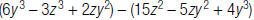
| 1. Multiply the second | |
| polynomial by –1. | 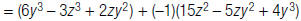 |
| 2. Distribute the –1. | 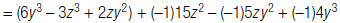 |
| 3. Simplify. | 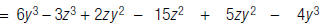 |
| 4. Write like terms next | |
| to each other. | 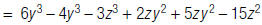 |
| 5. Combine like terms. | 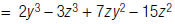 |
| To find the opposite of a polynomial, multiply each term by –1. When you add the opposite, the result is the same as changing the sign of each term in the polynomial being subtracted. |
| Answers to Sample Problems
b. –2, –2 b. 3x2, 5xy2, 3
|
Sample Problems
1. Evaluate the polynomial 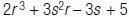 when r = 5 and s
= –2.
when r = 5 and s
= –2.
| Evaluate: | 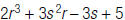 |
 a. Replace r
with 5. a. Replace r
with 5. |
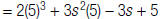 |
 b. Replace s
with –2. b. Replace s
with –2. |
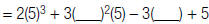 |
 c. Calculate. c. Calculate. |
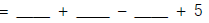 |
 |
2. Find: 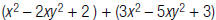
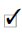 a. Remove the
parentheses. a. Remove the
parentheses. |
 |
 b. Write like
terms next to b. Write like
terms next toeach other. |
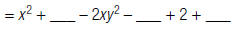 |
 c. Combine like
terms. c. Combine like
terms. |
 |
3. Find: 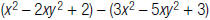
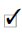 a. Multiply
each term in the second a. Multiply
each term in the secondpolynomial by –1. |
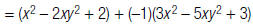 |
 b. Distribute
the –1. b. Distribute
the –1. |
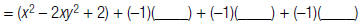 |
 c. Simplify. c. Simplify. |
 |
 d. Write like
terms next to each other. d. Write like
terms next to each other. |
 |
 e. Combine like
terms. e. Combine like
terms. |
 |
MULTIPLYING AND DIVIDING
Summary
Multiplying Monomials
Monomials are easy to multiply because they each have only one term.
To multiply monomials:
1. Rearrange the factors so that the constants are next to each other and the
factors with
the same base are next to each other.
2. Multiply.
For example, to find: 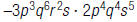
| 1. Rearrange the factors. | 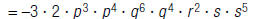 |
| 2. Multiply. | 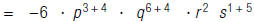 |
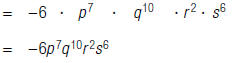 |
Multiplying a Monomial by a Polynomial with More Than
One Term
When multiplying a monomial by a polynomial with more than one term, you need to
multiply every term in the polynomial by the monomial.
To multiply a monomial by a polynomial with more than one term:
1. Distribute the monomial to each term in the other polynomial.
2. Simplify.
For example, to find:
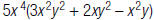
| 1. Distribute the monomial. | 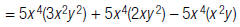 |
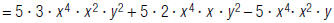 |
|
| 2. Simplify. | 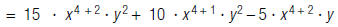 |
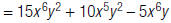 |
| In general, to multiply a monomial by a polynomial with more than one term: a(b + c + d) = a· b + a· c + a ·d |
| Remember: When
The y is on the bottom since the |
Dividing Monomials
To divide monomials:
1. Write the division as a fraction.
2. Cancel common numerical factors.
3. Divide factors with the same base by subtracting exponents.
For example, to find 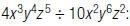
| 1. Write the division as a fraction. | 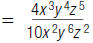 |
| 2. Cancel common numerical factors. | 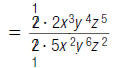 |
| 3. Divide factors with the same base. | 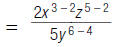 |
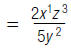 |
Dividing a Polynomial with More Than One Term by a
Monomial
When you divide a polynomial with more than one term by a monomial, you must
divide
each term of the polynomial by the monomial.
Use this rule :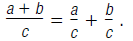
To divide a polynomial with more than one term by a
monomial:
1. Write the division as a fraction.
2. Rewrite the fraction using the rule 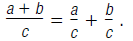
3. Perform the division on each of the resulting terms.
For example, to find 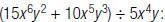
| 1. Write the division as a fraction. | 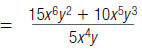 |
| 2. Rewrite the fraction using the rule |  |
| 3. Divide each of the resulting terms. | 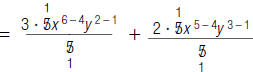 |
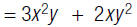 |
Sample Problems
1. Find: 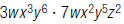
![]() a.
Rearrange the factors so the constants
a.
Rearrange the factors so the constants
are next to each other and factors with
the same base are next to each other.
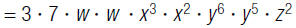
![]() b.
Multiply factors with the same
b.
Multiply factors with the same
base by adding the exponents.
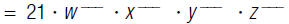
2. Find: pr 2s (p 2r + pr3s6 – 2)
![]() a.
Distribute the monomial.
a.
Distribute the monomial.

![]() b.
Multiply each of the
b.
Multiply each of the
resulting terms.
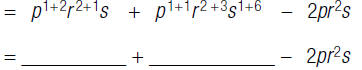
3. Find: 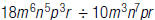
![]() a.
Write the division as a fraction.
a.
Write the division as a fraction.
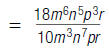
![]() b.
Cancel common numerical factors.
b.
Cancel common numerical factors.
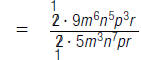
![]() c.
Divide factors with the same base by
c.
Divide factors with the same base by
subtracting exponents.
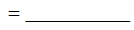
4. Find: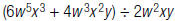
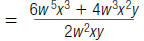 |
|
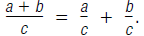 |
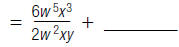 |
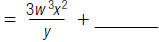 |
| Answers to Sample Problems b. 2, 5, 11, 2
|
HOMEWORK
Homework Problems
Circle the homework problems assigned to you by the computer, then complete them
below.
Explain
Adding and Subtracting
1. Circle the algebraic expression that is a polynomial.
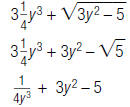
2. Write m beside the monomial, b beside the binomial, and
t
beside the trinomial.
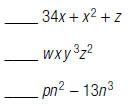
3. Given the polynomial
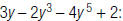
a. write the terms in descending order.
b. find the degree of each term.
c. find the degree of the polynomial.
4. Find: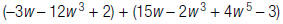
5. Find: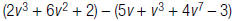
6. Evaluate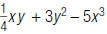 when x = 2
and y = 4.
when x = 2
and y = 4.
7. Find:
8. Find:
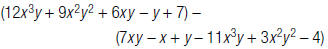
9. Angelina works at a pet store. Today, she is cleaning
three
fish tanks. These polynomials describe the volumes of the
tanks:
Tank1:x y2
Tank 2: 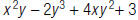
Tank 3: 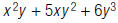
Write a polynomial that describes the total volume of the
three tanks.
Hint: Add the polynomials.
volume = ________
10. Angelina has three fish tanks to clean. These polynomials
describe their volumes.
Tank 1: xy2
Tank 2: x2y – 2y3 + 4xy2+ 3
Tank 3: x2y + 5xy2 + 6y3
What is the total volume of the fish tanks if x = 3 feet
and y = 1.5 feet?
volume = ________ cubic feet
11. Find:
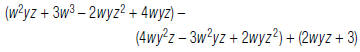
12. Find:
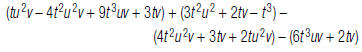
Multiplying and Dividing
13. Find: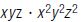
14. Find: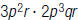
15. Find: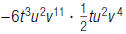
16. Find: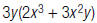
17. Find: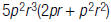
18. Find: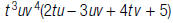
19. Write: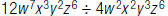 as a fraction
and simplify .
as a fraction
and simplify .
20. Write: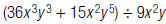 as a fraction
and simplify.
as a fraction
and simplify.
21. Find: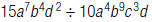
22. Tony is an algebra student. This is how he answered a
question on a test:
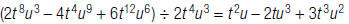
Is his answer right or wrong? Why? Circle the most
appropriate response.
The answer is right.
The answer is wrong. Tony divided the exponents rather
than adding them. The correct answer is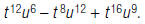
The answer is wrong. The terms need to be ordered by
degree. The correct answer is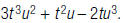
The answer is wrong. Tony divided the exponents rather
than subtracting them. The correct answer is
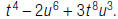
The answer is wrong. Tony shouldn't have canceled the
numerical coefficients. The correct answer is
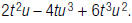
23.Find: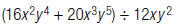
24.Find: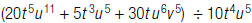
APPLY
Practice Problems
Here are some additional practice problems for you to try.
Adding and Subtracting
1. Circle the algebraic expressions below that are polynomials.
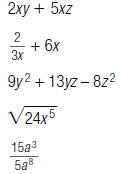
2. Circle the algebraic expressions below that are polynomials.
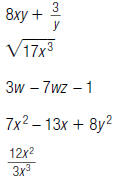
3. Identify each polynomial below as a monomial, a
binomial, or
a trinomial.
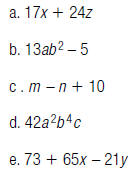
4. Identify each polynomial below as a monomial, a
binomial, or
a trinomial.
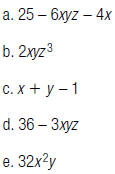
5. Find the degree of the polynomial
6. Find the degree of the polynomial
7. Find the degree of the polynomial
8. Evaluate 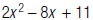 when x =
–1.
when x =
–1.
9. Evaluate 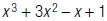 when x = –2.
when x = –2.
10. Evaluate 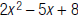 when x = 3.
when x = 3.
11. Evaluate 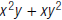 when x = 2 and y = –3.
when x = 2 and y = –3.
12. Evaluate 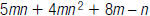 when m 4 and n –2.
when m 4 and n –2.
13. Evaluate 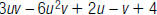 when u 2 and v –4.
when u 2 and v –4.
14. Find: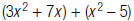
15. Find: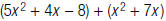
16. Find: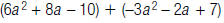
17. Find:
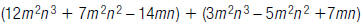
18. Find:
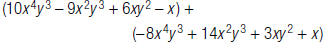
19. Find:
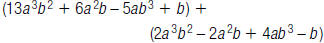
20. Find: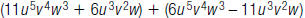
21. Find:
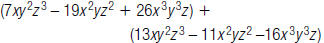
22. Find:
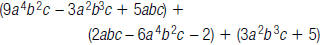
23. Find: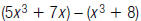
24. Find: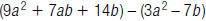
25. Find: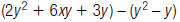
26. Find: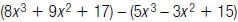
27. Find: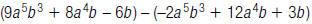
28. Find: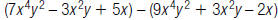
Multiplying and Dividing
29. Find: 3y2 ·5y
30. Find: 5x3 ·2x
31. Find: –5a5 ·9a4
32. Find: –3x3 ·12x 4
33. Find: 4x2y 5 ·7xy3
34. Find: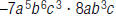
35. Find: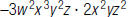
36. Find: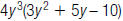
37. Find: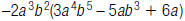
38. Find: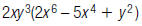
39. Find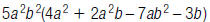
40. Find: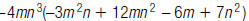
41. Find: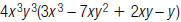
42. Find: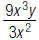
43. Find: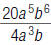
44. Find: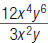
45. Find: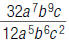
46. Find: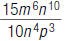
47. Find: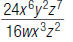
48. Find: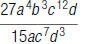
49. Find: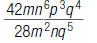
50. Find: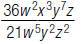
51. Find: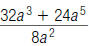
52. Find: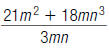
53. Find: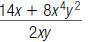
54. Find: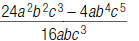
55. Find: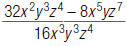
56. Find: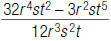
EVALUATE
Practice Test
Take this practice test to be sure that you are prepared for the final quiz in
Evaluate.
1. Circle the expressions that are polynomials.
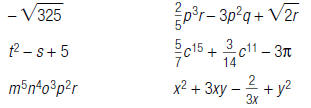
2. Write m beside the monomial(s), b beside the binomial(s),
and
t beside the trinomial(s).
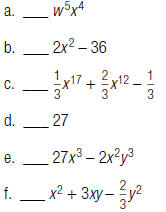
3. Given the polynomial
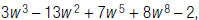 write
write
the terms in descending order by degree.
4. Find:
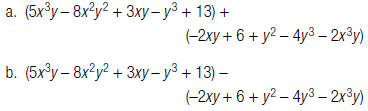
5. Find: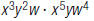
6. Find: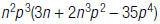
7. Find: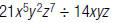
8. Find: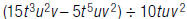
| Prev | Next |
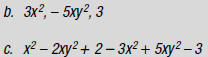
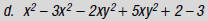
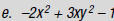 (in any order)
(in any order)