Polynomials in One Variable
An expression of the form
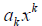
where k is a whole number and 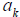 is a constant,
is
is a constant,
is
called a monomial. A sum of monomials forms a
polynomial where each monomial is called a term.
Polynomial in Standard Form:
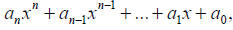
where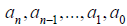 are coefficients, and n ≥ 0 is an
are coefficients, and n ≥ 0 is an
integer.
If 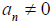 , then
, then
n – degree,
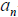 – leading coefficient,
– leading coefficient,
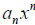 – leading term.
– leading term.
Polynomial? Yes/No Coefficients Degree
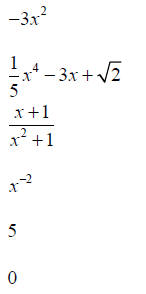
Adding and Subtracting Polynomials
Polynomials are added and subtracted by combining
like terms. The like terms are the monomials which
may differ only by the coefficients.
Example. Perform the indicated operation .
(3x4 + 2x3 − x) − (−x4 + x2 + x −1) =
Two polynomials are multiplied by using Properties of
Real Numbers and Laws of Exponents .
Example: (4x5 ) ∙ (3x2 ) =
Example: Find the product.
(2x4 − 3x2 +1)(4x3 − x) =
Use FOIL when multiplying two binomials.
(FOIL – First, Outer, Inner, Last)
( y − 3)(2y + 5) =
Special Products and Factoring
(x − y)(x + y) =
Squares of Binomials, or Perfect Squares:
(x + y)2 =
(x − y)2 =
Cubes of Binomials , or Perfect Cubes:
(x + y)3 =
(x − y)3 =
Difference of Two Cubes:
(x − y)(x2 + xy + y2 ) =
Sum of Two Cubes:
(x + y)(x2 − xy + y2 ) =
Factoring is a process of finding polynomials whose
product is equal to a given polynomial.
Example: Expand or factor by using the special product
formulas :
(a) (x + 3)(3− x) =
64x2 − 81=
(b) (7x + 5)2 =
4x2 + 28x + 49 =
(c) (2 − x)(4 + 2x + x2 ) =
8c3 + 27 =
(d) (2x − 3)3 =
Factoring out the Common Factor :
The CF of a polynomial is formed as a product of the
factors (numbers, variables , and/or expressions)
common to all terms, each raised to the smallest power
that appears on that factor in the polynomial.
Remember when factoring out the CF, we use the
Distributive property
ab + ac = a(b + c)
that is, we divide each term by the CF.
Example:
8x5 y3 + 6xy9 =
5x2 (x − 2)3 + x(x − 2)2 =
Factoring by Grouping
This method is used when the terms can be collected in
two or more groups such that there is a common factor
in all groups.
Example: Factor by grouping.
2x3 − 5x2 − 8x + 20 =
Prime (Irreducible) Polynomials
A polynomial is called prime or irreducible over a
specified set of numbers if it cannot be written as a
product of two other polynomials whose coefficients
are from the specified set.
A polynomial is considered to be factored completely
over the particular set of numbers if it is written as a
product of prime over that set polynomials.
Example: Determine which of the polynomials below
is/are prime over the real numbers
x2 + 9
y2 −10
Factoring a Second-Degree Trinomial
FOIL “in reverse” can be used for factoring the
trinomials over the integers.
(ax + b)(cx + d ) = ac ∙ x2 + (ad + bc) ∙ x + bd
Example: Factor the trinomials.
2x2 + 5x − 3 =
6x2 −17x +12 =
Factoring by substitution
Example: 16(x +1)2 + 8(x +1) +1=
Example: Factor completely over the integers by any
method.
(x −1)3 − 64 =
x6 + 7x3 − 8 =
5(3 − 4x)2 − 8(3 − 4x)(5x −1) =
b6 − 27 =
x6 − y6 =
Polynomial Division
Long Division 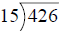
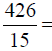
426 =
Check: Dividend = (Quotient)(Divisor) + Remainder
Dividing by a monomial:
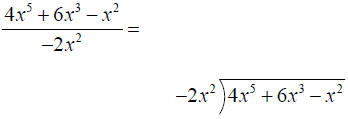
Dividing two polynomials with more than one term:
(1) Write terms in both polynomials in descending
order according to degree.
(2) Insert missing terms in both polynomials with a 0
coefficient.
(3) Use Long Division algorithm. The remainder is a
polynomial whose degree is less than the degree of
the divisor.
Example: Perform the division.
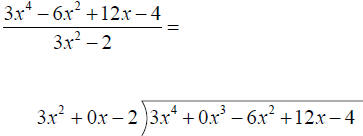
Synthetic Division
Synthetic division is used when a polynomial is divided
by a first-degree binomial of the form x − k .
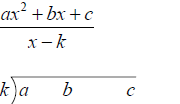 ←Coefficients of Dividend
←Coefficients of Dividend
Diagonal pattern: Multiply by k
Vertical pattern: Add terms
Example: Use synthetic division to find the quotient
and remainder.
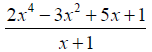
Example: Verify that x − 3 is a factor of
x3 + x2 −10x − 6
| Prev | Next |