Practice problems - Real Number System
1. If r is a rational number , (r ≠
0) and x is an irrational number, prove that
r + x and rx are irrational.
Solution : Since the set of all rational numbers, Q is a field, −r is also a
rational number . Now, if r + x is rational, then x = (−r) + (r + x) must also
be a rational number due to the field axioms. But, x is irrational. Hence,
r + x cannot be rational. Similarly, one can show that rx is also rational.
2. Prove that there is no rational number whose square is
12.
Solution Suppose that there is a rational number whose square is 12. Since 4
is a factor for 12, let such a rational number be 2r where r is again a rational
number. This implies, r2 = 3. Suppose r = m/n in its lowest terms. Observe
that neither m nor n can be even. For, if m is even, say, m = 2k we have
4k2 = 3n2 implying n is even. (why?) Thus, both m and n are odd. Let
m = 2s +1 and n = 2t+1. We then have, (2s +1)2 = 3(2t+1)2. This implies,
2s2 + 2s = 6t2 + 6t + 1 and this is a contradiction.
3. Let E be a non empty subset of an ordered set ; Suppose
α is a lower bound of
E and β is an upper bound of E. Prove that 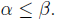
Solution : Let 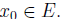 Then we have
Then we have
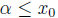 and
and 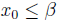 . Transitive property
. Transitive property
of order , implies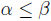
4. Let A be a non empty set of real numbers which is
bounded below. Let −A be
the set of all numbers −x where x ∈A. Prove that inf A = - sup(−A).
Solution : Let α=inf A. For any x ∈A, 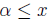 This implies,
This implies,
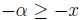 for all
for all
−x ∈−A. This means −α is an upper bound of (−A). Also, If
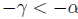 then
then
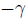 cannot be an upper bound of −A. For if it is, then
cannot be an upper bound of −A. For if it is, then
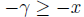 for all
for all
−x ∈(−A). This implies, 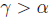 and is a lower bound of A which is not
and is a lower bound of A which is not
possible since is the inf A.
5. If 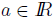 is such that
is such that
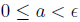 for every
for every 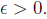 . Show that a
= 0.
. Show that a
= 0.
Solution: Let a > 0. Let 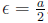 . This implies 0 < a < a/2 by assumption.
. This implies 0 < a < a/2 by assumption.
Clearly, this is impossible.
6. Let 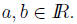 Suppose that for every
Suppose that for every
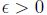 we have
we have 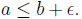 Show that
Show that 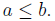
Solution: Suppose a > b. Then 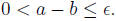 One can see this is impossible,
One can see this is impossible,
by choosing 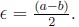
7. Let u be an upper bound of a non empty set S of IR.
Prove that u is the
supremum of S if and only if for every 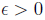 there
exists a
there
exists a 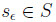 such that
such that
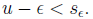
Solution: Since u is an upper bound of S we have
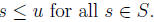
Suppose u = supS. Then, for any 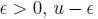 is not an upper bound of S, and
is not an upper bound of S, and
hence there exists an element 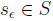 such that
such that
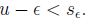 Conversely, the
Conversely, the
condition given implies that no number less than u can be an upper bound.
Hence, u is the least upper bound of S.
8. If 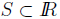 contains one of its upper bounds, show that
this upper bound of S is
contains one of its upper bounds, show that
this upper bound of S is
the supremum of S.
Solution: Suppose that 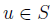 is an upper bound of S but not the supremum
is an upper bound of S but not the supremum
of S. Let 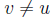 be the supremum of S. Then,
be the supremum of S. Then,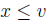 for all x
for all x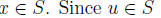
we have u < v. There exists a 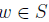 such that u < w. But this contradicts
such that u < w. But this contradicts
the fact that u is an upper bound of S.
9. Let A and B be bounded subsets of IR. Show that
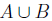 is bounded. Show
is bounded. Show
that sup (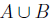 ) = max {sup A, sup B}.
) = max {sup A, sup B}.
Solution: Let 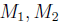 be real numbers such that
be real numbers such that
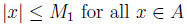 and
and
|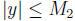 for all
for all 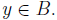 Define M = max {
Define M = max {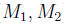 }. Then,
}. Then,
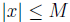 for all
for all
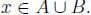 . So,
. So, 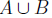 is bounded. Further: Let sup A = u and sup B = v and
is bounded. Further: Let sup A = u and sup B = v and
w = max{u, v}. For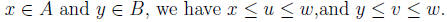
Then, w is an upper bound of 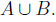 If z is an upper bound of
If z is an upper bound of
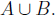 then z
then z
is an upper bound of A and B. And, 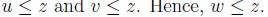
Therefore, w = (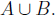 ).
).
10. Let S be a non empty subset of IR that is bounded
above. For any 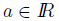
define 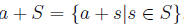 Prove that sup (a + S) = a+ sup S.
Prove that sup (a + S) = a+ sup S.
Solution: Let u = sup S, then 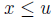 for all
for all
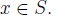 . Then,
. Then, 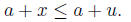
Thus, a + u is an upper bound for the set a + S. Thus,
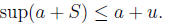
Now, if v is any upper bound of the set a + S then
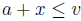 for all
for all 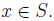
Consequently, 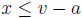 for all
for all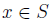 so that v − a is an upper bound of S.
so that v − a is an upper bound of S.
Then u = sup 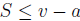 and so,
and so,
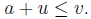 Since v is any upper bound of
Since v is any upper bound of
a + S and sup(a + S) is also an upper bound, we have
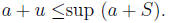
| Prev | Next |