Quadratic Functions
Definition: A quadratic function is a function
which can be put in the form
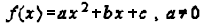 (General Form) or
(General Form) or
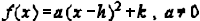 (Standard or Vertex Form )
(Standard or Vertex Form )
For a quadratic functions 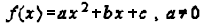 or :
or :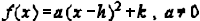
0) The domain of a quadratic function is 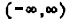
1) Graph : a (vertical) parabola
2) Opens up if 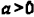
3) Opens down if 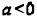
4) Vertex: 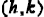 with
with
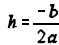 and
and 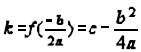
5) The x- intercept (s) can be found by setting 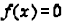 and solving for x .
and solving for x .
6) The y- intercept an be found by setting 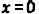 and solving for y .
and solving for y .
Remark: The above items can be used to sketch the graph of a quadratic
function
Examples:
Remark: The conversion from vertex form to general
from is very easy. For conversion from general form to vertex form
we use the method of Completing Square .
Example:
The Maximum and the Minimum of a Quadratic Function (Parabola):
As was discussed above, the vertex of a parabola is
![]() with
with
![]() and
and
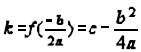
a) If the parabola opens up, the vertex will be the lowest point and we say that
the parabola has the minimum value
of 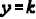 at
at 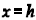 .
.
b) If the parabola opes down, the vertex will be the highest point and we say
that the parabola has the maximum
value of 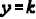 at
at 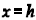 .
.
Remark: The coordinates
![]() of the vertex can be
found by a graphing calculator .
of the vertex can be
found by a graphing calculator .
Examples:
Application:
| Prev | Next |