Strand Trace Geometry

Performance Indicators Organized by Grade Level and Band under Major Understandings

Students will use visualization and spatial reasoning to analyze characteristics and properties of geometric shapes.
PK.G.1 Shapes	Match shapes, first with same size and orientation, then with different sizes and orientation.
PK.G.2 Shapes	Informally play with solids (e.g., building blocks).
K.G.1 Shapes	Describe characteristics and relationships of geometric objects.
1.G.1 Shapes	Match shapes and parts of shapes to justify congruency.
1.G.2 Shapes	Recognize, name, describe, create, sort, and compare two-dimensional and three-dimensional shapes.
2.G.1 Shapes	Experiment with slides, flips, and turns to compare two-dimensional shapes.
2.G.2 Shapes	Identify and appropriately name two-dimensional shapes: circle, square, rectangle, and triangle (both regular and irregular).
2.G.3 Shapes	Compose (put together) and decompose (break apart) two-dimensional shapes.
3.G.1 Shapes	Define and use correct terminology when referring to shapes (circle, triangle, square, rectangle, rhombus, trapezoid, and hexagon).
3.G.2 Shapes	Identify congruent and similar figures.
3.G.3 Shapes	Name, describe, compare, and sort three-dimensional shapes: cube, cylinder, sphere, prism, and cone.
3.G.4 Shapes	Identify the faces on a three-dimensional shape as two-dimensional shapes.
4.G.1 Shapes	Identify and name polygons, recognizing that their names are related to the number of sides and angles (triangle, quadrilateral, pentagon, hexagon, and octagon).
4.G.2 Shapes	Identify points and line segments when drawing a plane figure.
4.G.3 Shapes	Find perimeter of polygons by adding sides.
4.G.4 Shapes	Find the area of a rectangle by counting the number of squares needed to cover the rectangle.
4.G.5 Shapes	Define and identify vertices, faces, and edges of three-dimensional shapes.
5.G.1 Shapes	Calculate the perimeter of regular and irregular polygons.
6.G.1 Shapes	Calculate the length of corresponding sides of similar triangles, using proportional reasoning.
6.G.2 Shapes	Determine the area of triangles and quadrilaterals (squares, rectangles, rhombi, and trapezoids) and develop formulas.
6.G.3 Shapes	Use a variety of strategies to find the area of regular and irregular polygons.
6.G.4 Shapes	Determine the volume of rectangular prisms by counting cubes and develop the formula.
6.G.5 Shapes	Identify radius, diameter, chords and central angles of a circle.
6.G.6 Shapes	Understand the relationship between the diameter and radius of a circle.

6.G.7 Shapes	Determine the area and circumference of a circle, using the appropriate formula.
6.G.8 Shapes	Calculate the area of a sector of a circle, given the measure of a central angle and the radius of the circle.
6.G.9 Shapes	Understand the relationship between the circumference and the diameter of a circle.
7.G.1 Shapes	Calculate the radius or diameter, given the circumference or area of a circle.
7.G.2 Shapes	Calculate the volume of prisms and cylinders, using a given formula and a calculator.
7.G.3 Shapes	Identify the two-dimensional shapes that make up the faces and bases of three-dimensional shapes (prisms, cylinders, cones, and pyramids).
7.G.4 Shapes	Determine the surface area of prisms and cylinders, using a calculator and a variety of methods.
8.G.0 Constructions	Construct the following, using a straight edge and compass: Segment congruent to a segment, Angle congruent to an angle, Perpendicular bisector, Angle bisector.

Performance Indicators Organized by Grade Level and Band under Major Understandings

Students will use visualization and spatial reasoning to analyze characteristics and properties of geometric shapes.
A.G.1 Shapes	Find the area and/or perimeter of figures composed of polygons and circles or sectors of a circle Note: Figures may include triangles, rectangles, squares, parallelograms, rhombuses, trapezoids, circles, semi-circles, quarter-circles, and regular polygons (perimeter only).
A.G.2 Shapes	Use formulas to calculate volume and surface area of rectangular solids and cylinders.
G.G.1 Shape	Know and apply that if a line is perpendicular to each of two intersecting lines at their point of intersection, then the line is perpendicular to the plane determined by them.
G.G.2 Shape	Know and apply that through a given point there passes one and only one plane perpendicular to a given line.
G.G.3 Shape	Know and apply that through a given point there passes one and only one line perpendicular to a given plane.
G.G.4 Shape	Know and apply that two lines perpendicular to the same plane are coplanar.
G.G.5 Shape	Know and apply that two planes are perpendicular to each other if and only if one plane contains a line perpendicular to the second plane.
G.G.6 Shape	Know and apply that if a line is perpendicular to a plane, then any line perpendicular to the given line at its point of intersection with the given plane is in the given plane.
G.G.7 Shape	Know and apply that if a line is perpendicular to a plane, then every plane containing the line is perpendicular to the given plane.
G.G.8 Shape	Know and apply that if a plane intersects two parallel planes, then the intersection is two parallel lines.
G.G.9 Shape	Know and apply that if two planes are perpendicular to the same line, they are parallel.
G.G.10 Shape	Know and apply that the lateral edges of a prism are congruent and parallel.
G.G.11 Shape	Know and apply that two prisms have equal volumes if their bases have equal areas and their altitudes are equal.
G.G.12 Shape	Know and apply that the volume of a prism is the product of the area of the base and the altitude.
G.G.13 Shape	Apply the properties of a regular pyramid, including: 1) lateral edges are congruent; 2) lateral faces are congruent isosceles triangles; and 3) volume of a pyramid equals one-third the product of the area of the base and the altitude.
G.G.14 Shape	Apply the properties of a cylinder, including: 1) bases are congruent; 2) volume equals the product of the area of the base and the altitude; and 3) lateral area of a right circular cylinder equals the product of an altitude and the circumference of the base.
G.G.15 Shape	Apply the properties of a right circular cone, including: 1) lateral area equals one-half the product of the slant height and the circumference of its base; and 2) volume is one-third the product of the area of its base and its altitude.
G.G.16 Shape	Apply the properties of a sphere, including: 1) the intersection of a plane and a sphere is a circle; 2) a great circle is the largest circle that can be drawn on a sphere; 3) two planes equidistant from the center of the sphere and intersecting the sphere do so in congruent circles; 4) surface area is 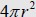; and 5) volume is .
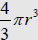G.G.17 Constructions	Construct a bisector of a given angle, using a straightedge and compass, and justify the construction.
G.G.18 Constructions	Construct the perpendicular bisector of a given segment, using a straightedge and compass, and justify the construction.
G.G.19 Constructions	Construct lines parallel (or perpendicular) to a given line through a given point, using a straightedge and compass, and justify the construction.
G.G.20 Constructions	Construct an equilateral triangle, using a straightedge and compass, and justify the construction.
G.G.21 Locus	Investigate and apply the concurrence of medians, altitudes, angle bisectors, and perpendicular bisectors of triangles.
G.G.22 Locus G.G.23 Locus	Solve problems using compound loci . Graph and solve compound loci in the coordinate plane .

Performance Indicators Organized by Grade Level and Band under Major Understandings

Students will identify and justify geometric relationships, formally and informally.
K.G.2 Relationships	Sort groups of objects by size and size order (increasing and decreasing).
2.G.4 Relationships	Group objects by like properties.
4.G.6 Relationships	Draw and identify intersecting, perpendicular, and parallel lines.
4.G.7 Relationships	Identify points and rays when drawing angles.
4.G.8 Relationships	Classify angles as acute, obtuse, right, and straight.
5.G.2 Relationships	Identify pairs of similar triangles.
5.G.3 Relationships	Identify the ratio of corresponding sides of similar triangles.
5.G.4 Relationships	Classify quadrilaterals by properties of their angles and sides.
5.G.5 Relationships	Know that the sum of the interior angles of a quadrilateral is 360 degrees.
5.G.6 Relationships	Classify triangles by properties of their angles and sides.
5.G.7 Relationships	Know that the sum of the interior angles of a triangle is 180 degrees.
5.G.8 Relationships	Find a missing angle when given two angles of a triangle.
5.G.9 Relationships	Identify pairs of congruent triangles.
5.G.10 Relationships	Identify corresponding parts of congruent triangles.
7.G.5 Relationships	Identify the right angle, hypotenuse, and legs of a right triangle.
7.G.6 Relationships	Explore the relationship between the lengths of the three sides of a right triangle to develop the Pythagorean Theorem.
7.G.7 Relationships	Find a missing angle when given angles of a quadrilateral.
7.G.8 Relationships	Use the Pythagorean Theorem to determine the unknown length of a side of a right triangle.
7.G.9 Relationships	Determine whether a given triangle is a right triangle by applying the Pythagorean Theorem and using a calculator.
8.G.1 Relationships	Identify pairs of vertical angles as congruent.
8.G.2 Relationships	Identify pairs of supplementary and complementary angles.
8.G.3 Relationships	Calculate the missing angle in a supplementary or complementary pair.
8.G.4 Relationships	Determine angle pair relationships when given two parallel lines cut by a transversal.
8.G.5 Relationships	Calculate the missing angle measurements when given two parallel lines cut by a transversal.

8.G.6 Relationships	Calculate the missing angle measurements when given two intersecting lines and an angle.
G.G.24 Proofs	Determine the negation of a statement and establish its truth value .
G.G.25 Proofs	Know and apply the conditions under which a compound statement (conjunction, disjunction, conditional, biconditional) is true.
G.G.26 Proofs	Identify and write the inverse, converse, and contrapositive of a given conditional statement and note the logical equivalences .
G.G.27 Proofs	Write a proof arguing from a given hypothesis to a given conclusion.
G.G.28 Proofs	Determine the congruence of two triangles by using one of the five congruence techniques (SSS, SAS, ASA, AAS, HL), given sufficient information about the sides and/or angles of two congruent triangles.
G.G.29 Proofs	Identify corresponding parts of congruent triangles.
G.G.30 Proofs	Investigate, justify, and apply theorems about the sum of the measures of the angles of a triangle.
G.G.31 Proofs	Investigate, justify, and apply the isosceles triangle theorem and its converse.
G.G.32 Proofs	Investigate, justify, and apply theorems about geometric inequalities, using the exterior angle theorem.
G.G.33 Proofs	Investigate, justify, and apply the triangle inequality theorem .
G.G.34 Proofs	Determine either the longest side of a triangle given the three angle measures or the largest angle given the lengths of three sides of a triangle.
G.G.35 Proofs	Determine if two lines cut by a transversal are parallel, based on the measure of given pairs of angles formed by the transversal and the lines.

Performance Indicators Organized by Grade Level and Band under Major Understandings

Students will identify and justify geometric relationships, formally and informally.
G.G.36 Proofs	Investigate, justify, and apply theorems about the sum of the measures of the interior and exterior angles of polygons.
G.G.37 Proofs	Investigate, justify, and apply theorems about each interior and exterior angle measure of regular polygons.
G.G.38 Proofs	Investigate, justify, and apply theorems about parallelograms involving their angles, sides, and diagonals.
G.G.39 Proofs	Investigate, justify, and apply theorems about special parallelograms (rectangles, rhombuses, squares) involving their angles, sides, and diagonals.
G.G.40 Proofs	Investigate, justify, and apply theorems about trapezoids (including isosceles trapezoids) involving their angles, sides, medians, and diagonals.
G.G.41 Proofs	Justify that some quadrilaterals are parallelograms, rhombuses, rectangles, squares, or trapezoids.
G.G.42 Proofs	Investigate, justify, and apply theorems about geometric relationships, based on the properties of the line segment joining the midpoints of two sides of the triangle.
G.G.43 Proofs	Investigate, justify, and apply theorems about the centroid of a triangle, dividing each median into segments whose lengths are in the ratio 2:1.
G.G.44 Proofs	Establish similarity of triangles, using the following theorems: AA, SAS, and SSS.
G.G.45 Proofs	Investigate, justify, and apply theorems about similar triangles.
G.G.46 Proofs	Investigate, justify, and apply theorems about proportional relationships among the segments of the sides of the triangle, given one or more lines parallel to one side of a triangle and intersecting the other two sides of the triangle.
G.G.47 Proofs	Investigate, justify, and apply theorems about mean proportionality: 1) the altitude to the hypotenuse of a right triangle is the mean proportional between the two segments along the hypotenuse; and 2) the altitude to the hypotenuse of a right triangle divides the hypotenuse so that either leg of the right triangle is the mean proportional between the hypotenuse and segment of the hypotenuse adjacent to that leg.
G.G.48 Proofs	Investigate, justify, and apply the Pythagorean theorem and its converse. G.G.49 Proofs Investigate, justify, and apply theorems regarding chords of a circle: 1) perpendicular bisectors of chords; and 2) the relative lengths of chords as compared to their distance from the center of the circle.
G.G.50 Proofs	Investigate, justify, and apply theorems about tangent lines to a circle: 1) a perpendicular to the tangent at the point of tangency; 2) two tangents to a circle from the same external point; and 3) common tangents of two non-intersecting or tangent circles.
G.G.51 Proofs	Investigate, justify, and apply theorems about the arcs determined by the rays of angles formed by two lines intersecting a circle when the vertex is : 1) inside the circle (two chords); 2) on the circle (tangent and chord); and 3) outside the circle (two tangents, two secants, or tangent and secant).
G.G.52 Proofs	Investigate, justify, and apply theorems about arcs of a circle cut by two parallel lines.
G.G.53 Proofs	Investigate, justify, and apply theorems regarding segments intersected by a circle: 1) along two tangents from the same external point; 2) along two secants from the same external point; 3) along a tangent and a secant from the same external point; and 4) along two intersecting chords of a given circle.

Performance Indicators Organized by Grade Level and Band under Major Understandings

Students will apply transformations and symmetry to analyze problem solving situations
1.G.3 Transform	Experiment with slides, flips, and turns of two-dimensional shapes.
1.G.4 Transform	Identify symmetry in two-dimensional shapes.
2.G.5 Transform	Explore and predict the outcome of slides, flips, and turns of two-dimensional shapes.
2.G.6 Transform	Explore line symmetry.
3.G.5 Transform	Identify and construct lines of symmetry.
5.G.11 Transform	Identify and draw lines of symmetry of basic geometric shapes.
8.G.7 Transform	Describe and identify transformations in the plane, using proper function notation (rotations, reflections, translations, and dilations).
8.G.8 Transform	Draw the image of a figure under rotations of 90 and 180 degrees.
8.G.9 Transform	Draw the image of a figure under a reflection over a given line.
8.G.10 Transform	Draw the image of a figure under a translation.
8.G.11 Transform	Draw the image of a figure under a dilation.
8.G.12 Transform	Identify the properties preserved and not preserved under a reflection, rotation, translation, and dilation.
G.G.54 Transform	Define, investigate, justify, and apply isometries in the plane (rotations, reflections, translations, glide reflections) Note: Use proper function notation.
G.G.55 Transform	Investigate, justify, and apply the properties that remain invariant under translations, rotations, reflections, and glide reflections.
G.G.56 Transform	Identify specific isometries by observing orientation, numbers of invariant points, and/or parallelism.
G.G.57 Transform	Justify geometric relationships (perpendicularity, parallelism, congruence) using transformational techniques (translations, rotations, reflections).
G.G.58 Transform	Define, investigate, justify, and apply similarities (dilations and the composition of dilations and isometries).
G.G.59 Transform	Investigate, justify, and apply the properties that remain invariant under similarities.
G.G.60 Transform	Identify specific similarities by observing orientation, numbers of invariant points, and/or parallelism.
G.G.61 Transform	Investigate, justify, and apply the analytical representations for translations, rotations about the origin of 90º and 180º, reflections over the lines x = 0 , y = 0 , and y = x , and dilations centered at the origin.

Performance Indicators Organized by Grade Level and Band under Major Understandings

Students will apply coordinate geometry to analyze problem solving situations.
K.G.5 Coordinate	Understand and use ideas such as over, under, above, below, on, beside, next to, and between.
1.G.5 Coordinate	Recognize geometric shapes and structures in the environment.
5.G.12 Coordinate	Identify and plot points in the first quadrant.
5.G.13 Coordinate	Plot points to form basic geometric shapes (identify and classify).
5.G.14 Coordinate	Calculate perimeter of basic geometric shapes drawn on a coordinate plane (rectangles and shapes composed of rectangles having sides with integer lengths and parallel to the axes.
6.G.10 Coordinate	Identify and plot points in all four quadrants.
6.G.11 Coordinate	Calculate the area of basic polygons drawn on a coordinate plane (rectangles and shapes composed of rectangles having sides with integer lengths).
7.G.10 Coordinate	Graph the solution set of an inequality (positive coefficients only) on a number line (See 7.A.5).
8.G.13 Coordinate	Determine the slope of a line from a graph and explain the meaning of slope as a constant rate of change.
8.G.14 Coordinate	Determine the y- intercept of a line from a graph and be able to explain the y-intercept.
8.G.15 Coordinate	Graph a line using a table of values.
8.G.16 Coordinate	Determine the equation of a line given the slope and the y-intercept.
8.G.17 Coordinate	Graph a line from an equation in slope-intercept form ( y = mx + b ).
8.G.18 Coordinate	Solve systems of equations graphically (only linear, integral solutions, y = mx + b format, no vertical/horizontal lines).
8.G.19 Coordinate	Graph the solution set of an inequality on a number line.
8.G.20 Coordinate	Distinguish between linear and nonlinear equations ax2 + bx + c; a=1 (only graphically).
8.G.21 Coordinate	Recognize the characteristics of quadratics in tables , graphs, equations, and situations.
A.G.3 Coordinate	Determine when a relation is a function, by examining ordered pairs and inspecting graphs of relations.
A.G.4 Coordinate	Identify and graph linear, quadratic (parabolic), absolute value, and exponential functions .
A.G.5 Coordinate	Investigate and generalize how changing the coefficients of a function affects its graph.
A.G.6 Coordinate	Graph linear inequalities.
A.G.7 Coordinate	Graph and solve systems of linear equations and inequalities with rational coefficients in two variables (See A.A.10).
A.G.8 Coordinate	Find the roots of a parabolic function graphically Note: Only quadratic equations with integral solutions.
A.G.9 Coordinate	Solve systems of linear and quadratic equations graphically. Note: Only use systems of linear and quadratic equations that lead to solutions whose coordinates are integers.

A.G.10 Coordinate	Determine the vertex and axis of symmetry of a parabola, given its graph (See A.A.41) Note: The vertex will have an ordered pair of integers and the axis of symmetry will have an integral value.
G.G.62 Coordinate	Find the slope of a perpendicular line, given the equation of a line.
G.G.63 Coordinate	Determine whether two lines are parallel, perpendicular, or neither, given their equations.
G.G.64 Coordinate	Find the equation of a line, given a point on the line and the equation of a line perpendicular to the given line.
G.G.65 Coordinate	Find the equation of a line, given a point on the line and the equation of a line parallel to the desired line.
G.G.66 Coordinate	Find the midpoint of a line segment, given its endpoints.
G.G.67 Coordinate	Find the length of a line segment, given its endpoints.
G.G.68 Coordinate	Find the equation of a line that is the perpendicular bisector of a line segment, given the endpoints of the line segment.
G.G.69 Coordinate	Investigate, justify, and apply the properties of triangles and quadrilaterals in the coordinate plane, using the distance, midpoint, and slope formulas.
G.G.70 Coordinate	Solve systems of equations involving one linear equation and one quadratic equation graphically.
G.G.71 Coordinate	Write the equation of a circle, given its center and radius or given the endpoints of a diameter.
G.G.72 Coordinate	Write the equation of a circle, given its graph Note: The center is an ordered pair of integers and the radius is an integer.
G.G.73 Coordinate	Find the center and radius of a circle, given the equation of the circle in center-radius form.
G.G.74 Coordinate	Graph circles of the form(x − h)² + ( y − k)² = r² .