Quadratic Functions

Definition: A quadratic function is a function which can be put in the form

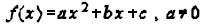(General Form) or 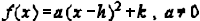(Standard or Vertex Form )

For a quadratic functions 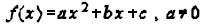or :

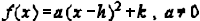
0) The domain of a quadratic function is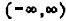

1) Graph : a (vertical) parabola

2) Opens up if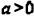

3) Opens down if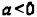

4) Vertex: 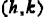with
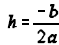and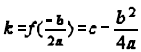
5) The x- intercept (s) can be found by setting 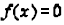and solving for x .

6) The y- intercept an be found by setting 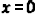and solving for y .

Remark: The above items can be used to sketch the graph of a quadratic function

Examples:

Remark: The conversion from vertex form to general from is very easy. For conversion from general form to vertex form
we use the method of Completing Square .

Example:

The Maximum and the Minimum of a Quadratic Function (Parabola):

As was discussed above, the vertex of a parabola is with

and

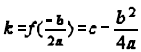
a) If the parabola opens up, the vertex will be the lowest point and we say that the parabola has the minimum value
of 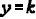at .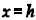


b) If the parabola opes down, the vertex will be the highest point and we say that the parabola has the maximum
value of 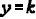at .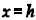

Remark: The coordinates of the vertex can be found by a graphing calculator .

Examples:

Application: