Rational Exponents
Overview
• Section 10.2 in the textbook:
– Simplifying rational exponents
– Simplifying rational exponent expressions
Simplifying Rational
Exponents
Rational Exponents
• Thus far, we have only seen integer
exponents
– Ex: 53, x-5
• Possible to have rational (i.e. fractional )
exponents
– Ex: 81/3, y-3/4
Rational Exponents vs Radical
Notation
• Relationship between rational exponents and
radical notation
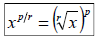 where p is the power and r
is
where p is the power and r
is
the radical index
Ex: 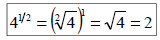
• Most calculators take only up to the third root
– How would we evaluate 
More on Rational Exponents
• Often helpful to write any negative
rational exponents as positive rational
exponents
• To evaluate rational exponents:
– Convert to radical notation and simplify if
possible
Simplifying Rational Exponents
(Example)
Ex 1: Convert to radical notation and
simplify:
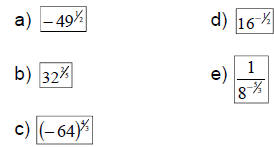
Simplifying Rational Exponent
Expressions
• Exponent rules for integer exponents
apply to rational exponents as well
– Remember them?
• Product : xa · xb = xa+b
• Quotient: xa / xb = xa-b
• Power : (xa)b = xab
Ex 2: Simplify – leave NO negative
exponents:

Ex 3: Use rational exponents to simplify the
following – leave the final answer in radical
notation:
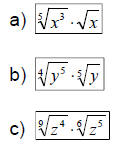
Summary
• After studying these slides, you should know
how to do the following:
– Simplify rational exponents
– Simplify rational expressions using the exponent rules
• Additional Practice
– See the list of suggested problems for 10.2
• Next lesson
– Simplifying Radical Expressions (Section 10.3)
| Prev | Next |