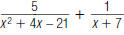RATIONAL EXPRESSIONS II
Here is what you'll learn in this
lesson:
Negative Exponents
a. Notation
b. Scientific notation
Multiplying and Dividing
a. Reducing a rational expression of the
form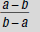
b. Multiplying rational expressions
c. Dividing rational expressions
d. Simplifying a complex fraction
Adding and Subtracting
a. Finding the least common
denominator of rational expressions
b. Adding rational expressions with
different denominators
c. Subtracting rational expressions with
different denominators
d. Simplifying a complex fraction
OVERVIEW
Rational expressions are fractions in which the numerator
and denominator are
polynomials.
In this lesson, you will learn more about how to multiply, divide, add, and
subtract rational
expressions. You will also learn about negative exponents.
EXPLAIN
NEGATIVE EXPONENTS
Summary
Negative Exponents
You have seen how to work with exponents that are positive integers or 0. Now
you will
learn about negative integer exponents.
For example, you have previously found 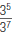 by
canceling:
by
canceling:

You can also find 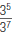 by
subtracting exponents:
by
subtracting exponents:
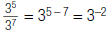
So,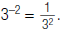
In general:
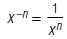
Here, x ≠ 0 and n is a nonnegative integer.
You can rewrite an expression with a negative exponent as a fraction by
following these steps:
1. Write the numerator as 1.
2. Write the denominator as the original expression, except change the negative
exponent to a positive exponent.
3. Do the multiplication in the denominator.
For example, to find 5-2:
1. Write the numerator as 1.
2. Write the denominator as the original
expression, except change the negative
exponent to a positive exponent.
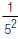
3. Do the multiplication in the denominator.
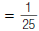
So,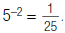
Even though the 5 is raised to a negative
power, the result is a positive num
Why does this work?
Well, since 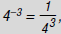 then
then
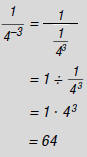
Notice that the 2-4 in the numerator
became the 24 in the denominator and
that the 5-3 in the denominator
became the 53 in the numerator.
Similarly, here’s how to simplify an expression raised to
a negative exponent that is in the
denominator of a fraction:
1. Take the expression out of the denominator and change the negative exponent
to a positive exponent.
2. Do the multiplication.
For example, to find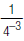 :
:
1. Take the expression out of the denominator and
change the negative exponent to a positive exponent.
43
2. Do the multiplication.
= 64
In general:
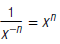
Here, x ≠ 0 and n is a nonnegative integer.
Properties of Negative Exponents
The basic properties of nonnegative exponents also hold for negative exponents.
The table
below summarizes some of these properties.
| Property | Positive Integer Exponent | Negative Integer Exponents |
| Multiplication | 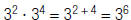 |
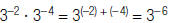 |
| Division | 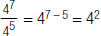 |
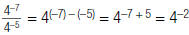 |
| Power of a Power | 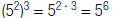 |
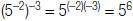 |
| Power of a Product | 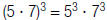 |
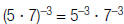 |
| Power of a Quotient | 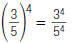 |
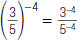 |
Some other properties that hold for negative exponents are
given below.
One property involving negative exponents shows how to rewrite a fraction in
which the
numerator and denominator are each raised to a negative power.
For example, here’s one way to rewrite using
only positive exponents:
using
only positive exponents:
In general:
Here, x ≠ 0, y ≠ 0, and m and n are nonnegative integers.
Another property involving negative exponents shows how to rewrite a fraction
that is
raised to a negative power.
For example, here’s one way to simplify
In general:
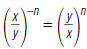
Here, x ≠ 0, y ≠ 0, and n is a nonnegative integer.
Simplifying Expressions with Negative Exponents
You can combine different properties to simplify more complicated expressions
containing
negative exponents.
For example, to rewrite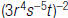 using only positive
exponents:
using only positive
exponents:
| 1. Use the Power of a Product Property . |
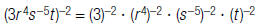 |
| 2. Use the Power of a Power Property. | 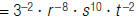 |
| 3. Rewrite the negative exponents as positive exponents. |
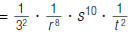 |
| 4. Simplify | 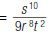 |
So,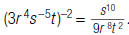
As another example, rewrite
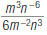 using only positive exponents:
using only positive exponents:
1. Since 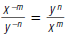 = ,
rewrite = ,
rewrite 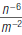 as . as .
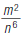 |
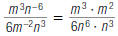 |
| 2. Use the Multiplication Property of Exponents. | 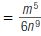 |
So, 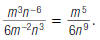
When a fraction is raised to a negative
power, flip the fraction and change the
negative power to positive.
Remember the decimal point is at the
end of a whole number. For example,
the number 239 can be written like this:
239.0
As a third example, to simplify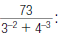
| 1. Rewrite using positive exponents. | 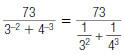 |
| 2. Multiply to eliminate the exponents. | 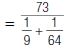 |
| 3. Rewrite each fraction in the denominator with the LCD, 576. |
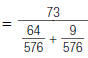 |
| 4. Add the fractions in the denominator | 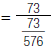 |
| 5. Simplify. | 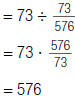 |
So,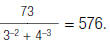
Scientific Notation
Now that you know how to work with negative exponents as well as positive
exponents,
you can learn how to use scientific notation. Scientific notation is a shorthand
that is often
used to write very small or very large numbers.
For example here are some very small and very large numbers:
• the gross national debt at the end of 1994 was $4,643,700,000,000
• a number called Planck’s constant that relates the energy of a photon to its
• frequency is 0.000000000000004135 electron volt seconds
• the speed of light is 299,792,500 meters per second
You can rewrite these numbers in scientific notation.
A number written in scientific notation is the product of a number between 1 and
10 and
an integer power of 10. To write a number in scientific notation:
1. Move the decimal point to the left or to the right until you have a number
between 1 and 10.
2. Multiply this number by a power of 10. To find the power, count the number
of places you moved the decimal point.
• If you moved the decimal point to the left, the power is positive.
• If you moved the decimal point to the right, the power is negative.
For example, to write $4,643,700,000,000, in scientific notation:
| 1. Move the decimal point to the left. |
 |
| 2. Multiply by the appropriate power of 10. |
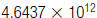 |
So, $4,643,700,000,000 =
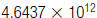 dollars.
dollars.
As another example. To write 0.000000000000004135 eVsec (electron volt seconds),
in
scientific notation:
| 1. Move the decimal point to the right. |
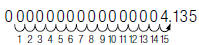 |
| 2. Multiply by the appropriate power of 10 |
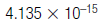 |
So, 0.000000000000004135 eVsec =
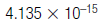 eVsec.
eVsec.
You can also reverse this process to write a number given in scientific notation
in
expanded form.
To write a number in expanded form you must perform the multiplication indicated
by the
power of 10 in scientific notation. So:
1. Move the decimal point the number of places indicated by the power of 10.
• If the power is positive, move the decimal point to the right.
• If the power is negative, move the decimal point to the left.
2. Fill in additional zeros as needed.
For example, to write 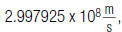 in expanded form:
in expanded form:
1. Move the decimal point
to the right 8 places.
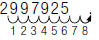
2. Fill in additional zeros
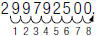
So,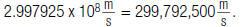
You moved the decimal point 12 places
to the left, so multiply by 1012.
Here’s a hint to help you know if
you’ve moved the decimal point in the
correct direction. If the power is
positive, the number should be big.
If the power is negative, the number
should be less than 1.
Answers to Sample Problems
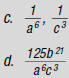
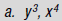
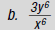
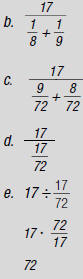

Sample Problems
1. Rewrite 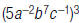 using only
positive exponents.
using only
positive exponents.
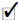 a. Use the
Power of a Product Property. a. Use the
Power of a Product Property. |
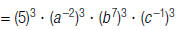 |
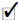 b. Use the
Power of a Power Property. b. Use the
Power of a Power Property. |
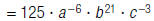 |
 c. Rewrite
using only positive exponents. c. Rewrite
using only positive exponents. |
 |
 d. Simplify. d. Simplify. |
 |
2. Rewrite 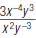 using only
positive exponents.
using only
positive exponents.
 a. Use a. Use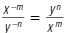 to =
to =rewrite 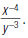 |
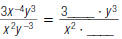 |
 b. Use the
Multiplication b. Use the
Multiplication of Exponents. |
= ______ |
3. Simplify this expression: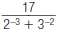
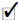 a. Rewrite
using only positive exponents a. Rewrite
using only positive exponents |
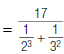 |
 b. Multiply to
eliminate the exponents. b. Multiply to
eliminate the exponents. |
= __________ |
 c. Rewrite
each fraction in the c. Rewrite
each fraction in thedenominator with the LCD. |
= __________ |
 d. Add the
fractions in the denominator. d. Add the
fractions in the denominator. |
= __________ |
 e. Simplify. e. Simplify. |
= __________ = __________ = ______ |
4. Write 45,318,000 in scientific notation.
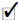 a. Move the decimal
point. = 4.5318000
a. Move the decimal
point. = 4.5318000
 b. Multiply by the appropriate power of 10. =
__________
b. Multiply by the appropriate power of 10. =
__________
5.Write 9.68 x 10-5 in expanded form.
 a. Move the decimal point. = __________
a. Move the decimal point. = __________
 b. Fill in additional zeros. = __________
b. Fill in additional zeros. = __________
MULTIPLYING AND DIVIDING
Summary
Reducing a Rational Expression of the Form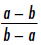
Look at this rational expression: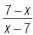
Here, the numerator and denominator are already factored,
and at first glance the rational
expression may appear to be in lowest terms.
But notice that the numerator and denominator are the same except for their
signs. To
reduce this rational expresson further:
| 1. Factor –1 out of either the numerator or the denominator. Here, the numerator is factored. |
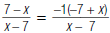 |
| 2. Rewrite (–7 + x ) as (x – 7). | 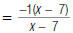 |
| 3. Cancel common factors. | 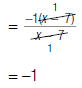 |
So,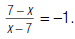
In general: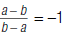
Here, a ≠ b.
Here’s another example. To reduce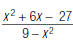
1. Factor the numerator and
denominator.
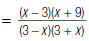
In the numerator, notice (x – 3).
In the denominator, notice (3 – x ).
2. Recall that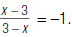 |
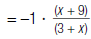 |
| So, you can rewrite the expression. | 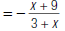 |
Multiplying Rational Expressions
You have learned how to multiply rational expressions. Here is an example.
Find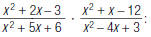
| 1. Factor the numerators and denominators. |
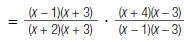 |
| 2. Cancel pairs of factors common to the numerators and denominators. |
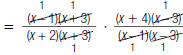 |
| 3. Multiply the numerators. Multiply the denominators. |
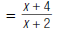 |
So,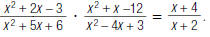
Dividing Rational Expressions
You have learned how to divide rational expressions by inverting the divisor and
then
multiplying. Here is an example.
Find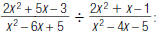
| 1. Invert the second fraction and change ÷ to . Then multiply. |
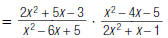 |
| 2. Factor the numerators and denominators. |
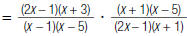 |
| 3. Cancel pairs of factors common to the numerators and denominators. |
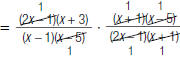 |
| 4. Multiply the numerators. Multiply the denominators. |
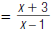 |
so,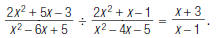
Simplifying a Complex Fraction
A fraction that contains other fractions is called a complex fraction. To
simplify a complex
fraction, start by rewriting the complex fraction as a division problem. Then
invert the
second fraction, and multiply.
For example, to simplify the complex fraction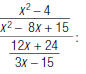
| 1. Rewrite the complex fraction as a division problem. |
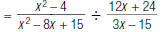 |
| 2. Divide by inverting the second fraction and multiplying. |
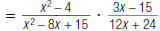 |
| 3. Factor the numerators and denominators. |
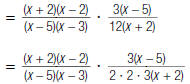 |
| 4. Cancel pairs of factors common to the numerators and denominators |
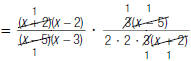 |
| 5. Multiply the numerators. Multiply the denominators. |
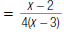 |
so,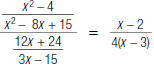
Sample Problems
1. Reduce to lowest terms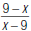
|
|
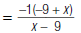 |
|
|
= _________ |
|
|
= _________ |
2. Reduce to lowest terms: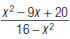
|
and denominator |
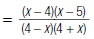 |
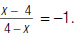 So rewrite the expression. |
= _____ _____ |
|
|
= ________ |
Answers to Sample Problems
Answers to Sample Problems
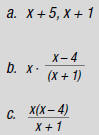
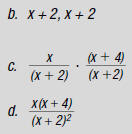
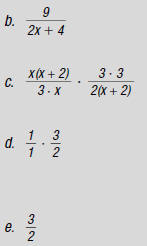
3. Find: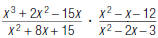
|
denominators. |
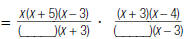 |
|
|
= _________ |
|
Multiply the denominators |
= ___________ |
4. Find: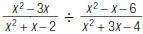
|
and change ÷ to |
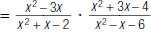 |
|
denominators. |
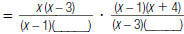 |
|
|
= _________ |
|
Multiply the denominators. |
= _________ |
5. Simplify this complex fraction: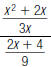
|
|
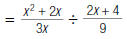 |
|
fraction and multiply.) |
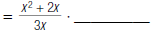 |
|
denominators. |
= _________ |
|
common to the numerator and denominator. |
= _________ |
|
Multiply the denominators. |
= _________ |
ADDING AND SUBTRACTING
Summary
Finding the Least Common Denominator (LCD) of Two or More
Rational Expressions
In order to add or subtract rational expressions with different denominators,
you need to
find the least common denominator (LCD) of the rational expressions. This LCD is
the least
common multiple (LCM) of the polynomials in the denominators . You can find the
LCM of a
collection of polynomials in the same way you find the LCM of a collection of
numbers.
To find the LCM of a collection of polynomials:
1. Factor each polynomial.
2. List each factor the greatest number of times it appears in any
factorization.
3. Find the product of these factors. This is the LCM.
For example, to find the LCM of
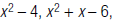 and
and 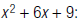
1. Factor each polynomial.
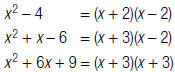
2. List each factor the greatest number
of times it appears in any factorization.
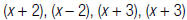
3. Find the product of these factors.
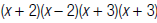
So, the LCM of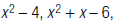 and
and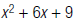 is
is
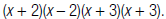
Remember, to find the LCM of a
collection of numbers:
1. Find the prime factorization of each
number.

2. List each prime factor the greatest
number of times it appears in any
factorization. 2, 3, 3, 5, 5
3. Find the product of these factors.
This is the LCM.
2 ·3 ·3· 5· 5 = 450
The LCM of a collection of polynomials is
usually left in factored form. You don't
have to do the multiplication.
Remember, to add fractions with
different denominators:
1. Factor each denominator into its
prime factors.
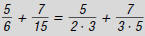
2. Find the LCD of both fractions. This
is the LCM of the denominators.
LCD = 2· 3· 5
3. Rewrite each fraction with this LCD.
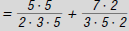
4. Add the numerators. Keep the
denominator the same.
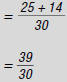
5. Factor and reduce the fraction to
lowest terms as appropriate .
so,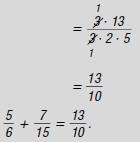
In the third step you may have been
tempted to cancel common factors. But
this would get you back to where you
started. Remember to add first, then
factor and cancel common factors.
Adding Rational Expressions with Different Denominators
You can add rational expressions with different denominators in much the same
way you
add fractions with different denominators. The key idea is to write the rational
expressions
with the same denominator.
To add rational expressions with different denominators:
1. Factor each denominator.
2. Find the LCM of the denominators. This is the LCD of the rational
expressions.
3. Rewrite each algebraic fraction with this LCD.
4. Add the numerators. The denominator stays the same.
5. Factor and reduce the rational expression to lowest terms as appropriate.
For example, to find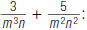
| 1. Factor each denominator: | 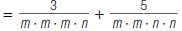 |
| 2. Find the LCD of the rational expressions |
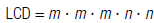 |
| 3. Rewrite each algebraic fraction with the LCD, m m m n n. |
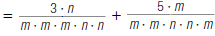 |
| 4. Add the numerators. The denominator stays the same. |
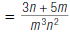 |
This rational expression is in lowest terms.
So,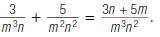
As another example, to find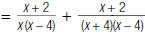
| 1. Factor each denominator | 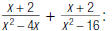 |
| 2. Find the LCD of the rational expressions. |
LCD = x (x + 4)(x – 4) |
| 3. Rewrite each algebraic fraction with the LCD, x (x – 4)(x + 4). |
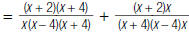 |
| 4. Add the numerators. The denominator stays the same |
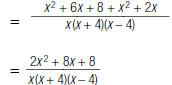 |
| 5. Factor and reduce the rational expression to lowest terms. |
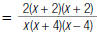 |
So,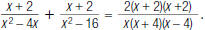
Subtracting Rational Expressions with Different
Denominators
You can subtract rational expressions with different denominators in much the
same way
you subtract fractions with different denominators. The key idea is to write the
rational
expressions with the same denominator.
To subtract rational expressions with different denominators:
1. Factor each denominator.
2. Find the LCM of the denominators. This is the LCD of the rational
expressions.
3. Rewrite each algebraic fraction with this LCD.
4. Subtract the numerators. The denominator stays the same.
5. Factor and reduce the rational expression to lowest terms as appropriate.
For example, to find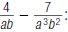
| 1. Factor each denominator: | 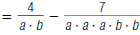 |
| 2. Find the LCD of the rational expressions. | 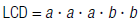 |
| 3. Rewrite each algebraic fraction with the LCD, a a a b b. |
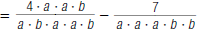 |
| 4. Subtract the numerators. The denominator stays the same. |
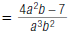 |
This rational expression is in lowest terms.
so,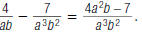
As another example, to find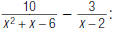
| 1. Factor each denominator: | 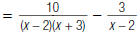 |
| 2. Find the LCD of the rational expressions. |
LCD = (x – 2)(x + 3) |
| 3. Rewrite each algebraic fraction with the LCD (x – 2)(x + 3). |
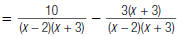 |
| 4. Subtract the numerators. The denominator stays the same. |
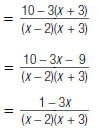 |
This rational expression is in lowest terms.
So,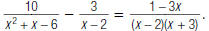
Remember, to subtract fractions with
different denominators:
1. Factor each denominator into its
prime factors.
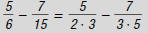
2. Find the LCD of both fractions. This
is the LCM of the denominators.
LCD = 2 ·3 ·5
3. Rewrite each fraction with this LCD.
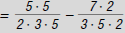
4. Subtract the numerators. Keep the
denominator the same.
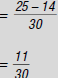
So,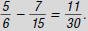
In the third step you may have been
tempted to cancel common factors.
But this would get you back to where
you started. Remember to subtract first,
then factor and cancel common factors.
Simplifying a Complex Fraction
Recall that a fraction that contains other fractions is called a complex
fraction. Here’s one
way to simplify certain complex fractions:
1. Perform any addition or subtraction in the numerator or denominator.
2. Rewrite the complex fraction as a division problem.
3. Divide.
For example, to find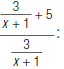
| 1. Perform the addition in the numerator. The least common denominator of 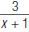 and 5 is (x+1) and 5 is (x+1) |
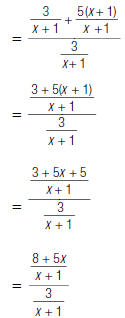 |
| 2. Rewrite the complex fraction as a division problem. |
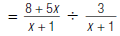 |
| 3. To divide, invert the second fraction and replace ÷with |
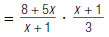 |
| 4. Cancel common factors. | 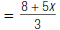 |
so,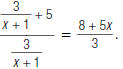
Sample Problems
1. Find the LCM of 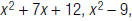 and
and
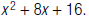
|
|
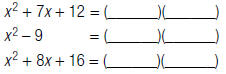 |
|
number of times it appears in any factorization. |
_____, _____, _____, ___ |
|
in the list. This is the LCM. |
(_____)(_____)(_____)(_____) |
2. Find: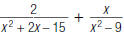
|
|
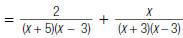 |
|
expressions. |
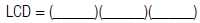 |
|
expression using this LCD. |
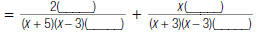 |
|
denominator stays the same. |
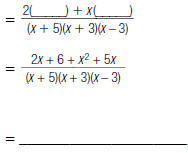 |
3. Find: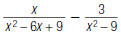
|
|
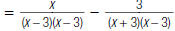 |
|
expressions. |
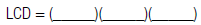 |
|
expression using this LCD. |
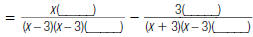 |
|
The denominator stays the same. |
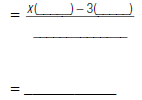 |
Answers to Sample Problems
a. x + 3, x + 4 (in either order)
x + 3, x – 3 (in either order)
x + 4, x + 4 (in either order)
b. x + 3, x – 3, x + 4, x + 4
(in any order)
c. (x + 3)(x – 3)(x + 4)(x + 4)
(in any order)
b. x + 5, x + 3, x – 3 (in any order)
c. top: x + 3, x + 5
bottom: x + 3, x + 5
d. x + 3, x + 5
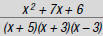 or
or
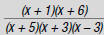
b. x – 3, x – 3, x + 3 (in any order)
c. top: x + 3, x – 3
bottom: x + 3, x – 3
d. top: x + 3, x – 3
bottom: (x – 3)(x – 3)(x + 3)
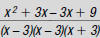 or
or
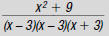
Answers to Sample Problems
b. z + 5, z – 5
c. top: z + 5, z – 5
bottom: z + 5, z – 5
d. top: z + 5, –1, z – 5
bottom: (z + 5)(z – 5)
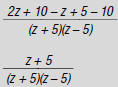
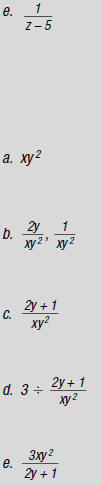
4. Find: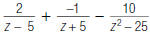
|
|
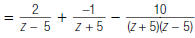 |
|
expressions. |
 |
|
expression using this LCD. |
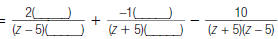 |
|
numerators. The denominator stays the same. |
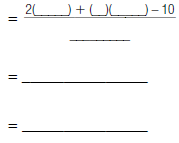 |
|
rational expression to lowest terms. |
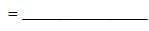 |
5. Simplify this complex fraction: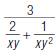
|
denominator, find the LCD. |
LCD = _____ |
|
this LCD. |
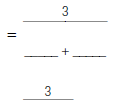 |
|
the denominator. |
= _____________ |
|
as a division problem. |
= _____________ |
|
|
= _____________ |
HOMEWORK
Homework Problems
Circle the homework problems assigned to you by the computer, then complete them
below.
Explain
Negative Exponents
1. Find: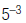
2. Find: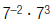
3. Find: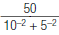
In problems 4 through 9, simplify each expression. Use
only
positive exponents in your answers.
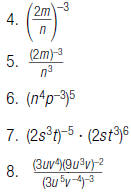
9. All matter is made up of tiny particles called atoms.
Through
experimentation, it has been found that the diameters of
atoms range from 1 x 10-8 cm to 5 x 10-8 cm. Rewrite
each of these numbers in expanded form.
10. The monthly payment E on a loan of amount P can be
computed by using the formula below, where r is the
monthly interest rate, and n is the number of months for
which the loan is made. Find the monthly payment on a
$15,000 loan for 4 years (48 months) if the monthly interest
rate is 1%.
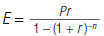
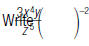 using only posi
using only posi
exponents.
12. Suppose x = 3 and y = 5.
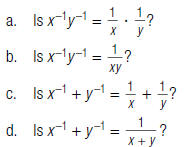
Multiplying and Dividing
13. Reduce to lowest terms: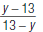
14. Reduce to lowest terms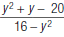
15. Find: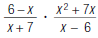
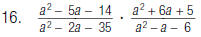
17. Find: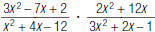
18. Find: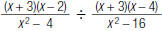
19. Find: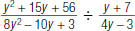
20. Find: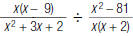
21. Find: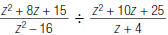
In Problems 22, 23 and 24, simplify the complex fractions.
Reduce your answer to lowest terms.
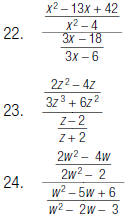
Adding and Subtracting
25. Find the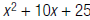 and
and
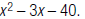
26. Find the LCM of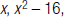 and
and
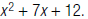
27. Find: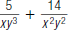
28. Find: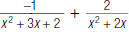
29. Find: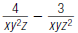
30. Find: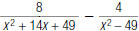
31. Find: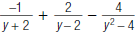
32. Find: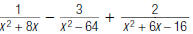
33. Simplify the left side of the equation below to show
it equals 1/n.
Then use the equation to find two fractions with 1 in the
numerator whose difference is 1/5. (Hint: let n = 5).
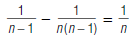
34. Optometrists use the formula below to find the
strength to
be used for the lenses of glasses. Simplify the right side of
this formula, then find the value of P that corresponds to
a = 12 and b = 0.3.
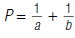
35. The total resistance, R, of a circuit that consists of
two
resistors connected in parallel with resistance R1 and R2
is
given by the formula below. Simplify this formula, then find
the resistance, R, if R1 = 3 ohms and R2 = 4 ohms.
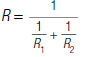
36. Simplify this complex fraction: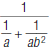
APPLY
Practice Problems
Here are some additional practice problems for you to try
Negative Exponents
1. Find: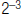
2. Find: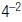
3. Find: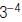
4. Find: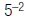
5. Find: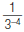
6. Find: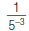
7. Find: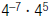
8. Find: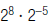
9. Find: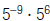
10. Find: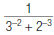
11. Find: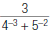
12. Find: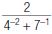
13. Rewrite using only positive exponents: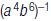
14. Rewrite using only positive exponents: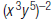
15. Rewrite using only positive exponents: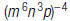
16. Rewrite using only positive exponents: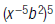
17. Rewrite using only positive exponents: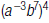
18. Rewrite using only positive exponents: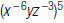
19. Rewrite using only positive exponents: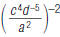
20. Rewrite using only positive exponents: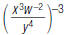
21. Rewrite using only positive exponents: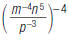
22. Rewrite using only positive exponents: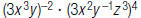
23. Rewrite using only positive exponents: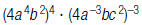
24. Rewrite using only positive exponents: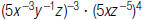
25. Write in scientific notation: 0.000057
26. Write in scientific notation: 148,000,000
27. The following number is written in scientific notation. Write it
in expanded form: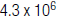
28. The following number is written in scientific notation. Write it
in expanded form: 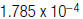
Multiplying and Dividing
29. Reduce to lowest terms: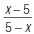
30. Reduce to lowest terms: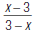
31. Reduce to lowest terms: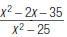
32. Reduce to lowest terms: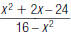
33. Reduce to lowest terms:
34. Reduce to lowest terms: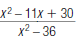
35. Reduce to lowest terms: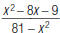
36. Find: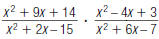
37. Find: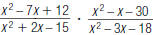
38. Find: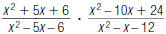
39. Find: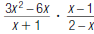
40. Find: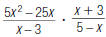
41. Find: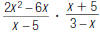
42. Find: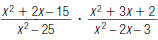
43. Find: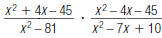
44. Find: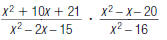
45. Find: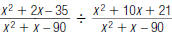
46. Find: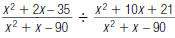
47. Find: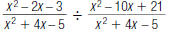
48. Find: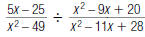
49. Find: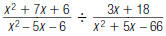
50. Find: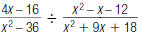
51. Simplify the complex fraction below. Write your answer
in
lowest terms.
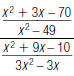
52. Simplify the complex fraction below. Write your answer
in
lowest terms.
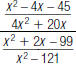
53. Simplify the complex fraction below. Write your answer
in
lowest terms.
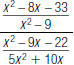
54. Simplify the complex fraction below. Write your answer
in
lowest terms.
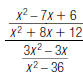
55. Simplify the complex fraction below. Write your answer
in
lowest terms.
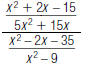
56. Simplify the complex fraction below. Write your answer
in
lowest terms.
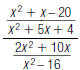
Adding and Subtracting
57. Find the LCM of 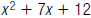 and
and
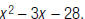
58. Find the LCM of 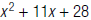 and
and
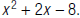
59. Find the LCM of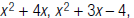 and
and
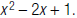
60. Find the LCM of 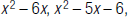 and
and
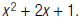
61. Find: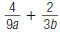
62. Find: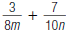
63. Find: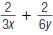
64. Find: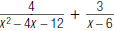
65. Find: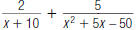
66. Find: