Related Rates
- The idea is to compute the rate of change of one quantity in terms of the
rate of change of another quantity
(which we may know more information about).
Suppose we want to compute the rate of change of the radius of a circle with
respect to time. Also
suppose we know the rate at which the area of the circle is changing with
respect to time.
- We will find an equation that relates the quantities, then differentiate with
respect to time using the chain rule.
So we find an equation that relates the area of a circle with its radius (
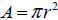 ). Then, we take the
). Then, we take the
derivative of both sides with respect to time, t, using the chain rule
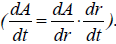
Steps in Solving Related Rates Problems
1. Read the problem carefully. If appropriate, draw a picture that represents
the situation.
2. Assign variables to quantities and write down what is known and what is
unknown.
3. Write an equation that relates quantities. (Often used: Pythagorean Theorem,
trigonometric relationships ,
similar triangles, formulas for volume and area, etc.)
4. Differentiate the equation with respect to time (we use the chain rule here )
5. Substitute known values in the resulting equation
6. Solve for the unknown .
7. Answer the question (make sure you answer the question being asked!!!)
Ex 1) You are blowing a bubble with bubble gum and can blow air into the bubble at a rate of 3 in3 / s .
a. How fast is the radius increasing with respect to time when r = 3 inches?
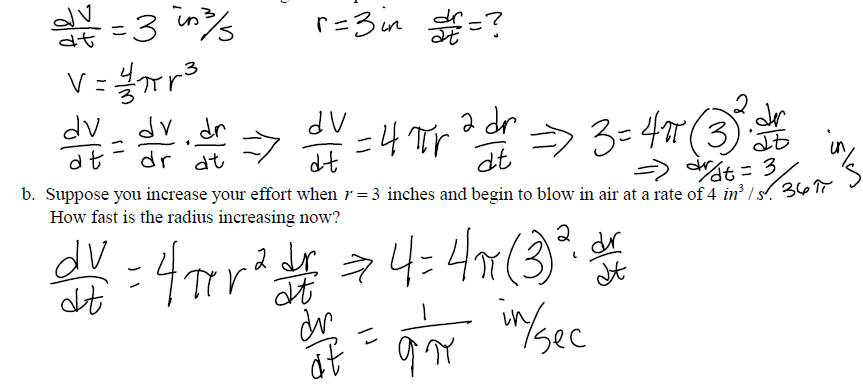
Ex 2) #4 p267 The length of a rectangle is increasing at a rate of 8 cm/s and
its width is increasing at a rate of 3
cm/s. When the length is 20cm and the width is 10cm, how fast is the area of the
rectangle increasing?
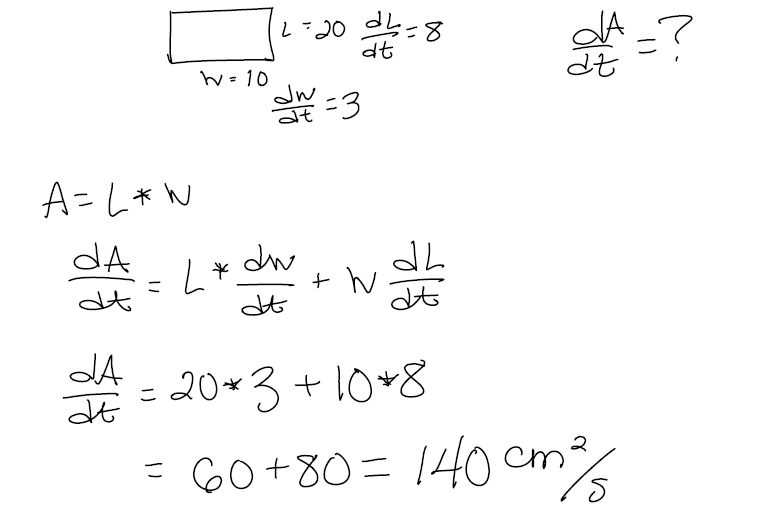
Ex 3) #10 p267 At noon, ship A is 150 km west of ship B. Ship A is sailing
east at 35 km/h and ship B is
sailing north at 25 km/h. How fast is the distance between the ships changing at
4:00 pm?
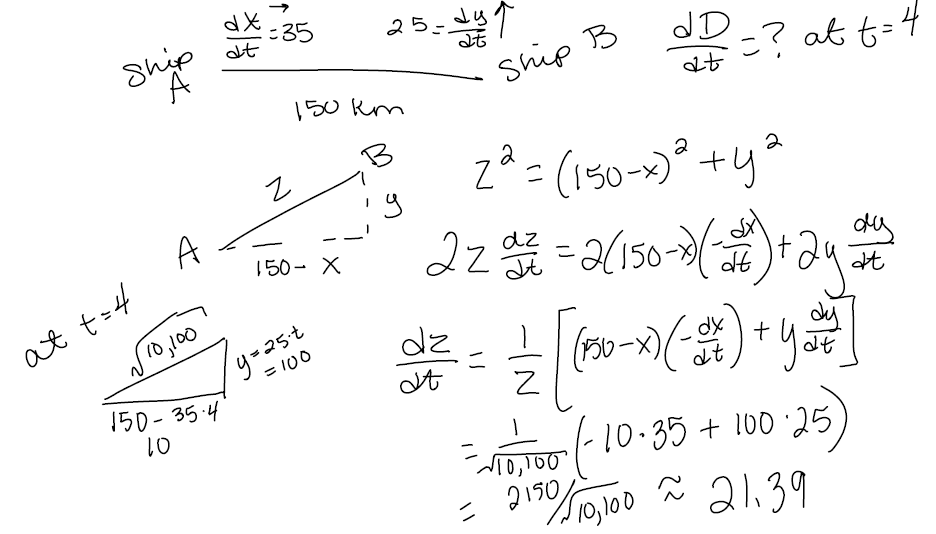
Ex 4) #26 p268 A kite 100 ft above the ground moves horizontally at a speed
of 8 ft/s. At what rate is the angle
between the string and the horizontal decreasing when 200 ft of string have been
let out?
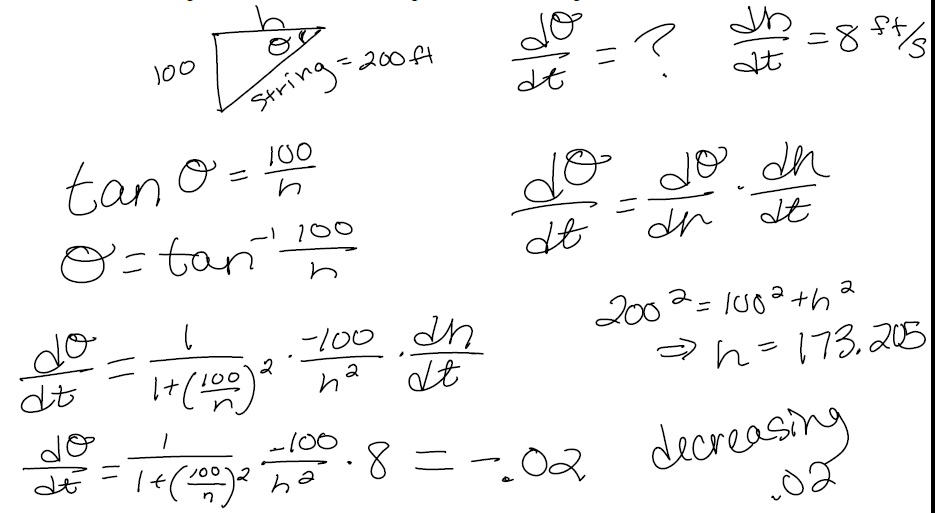
Ex 5) #22 p268 Water is leaking out of an inverted conical tank at a rate of
10,000 cm3 /min at the same time
that water is being pumped into the tank at a constant rate. The tank has height
6 m and the diameter at the
top is 4 m. If the water level is rising at a rate of 20 cm/min when the height
of the water is 2 m, find the
rate at which water is being pumped into the tank.
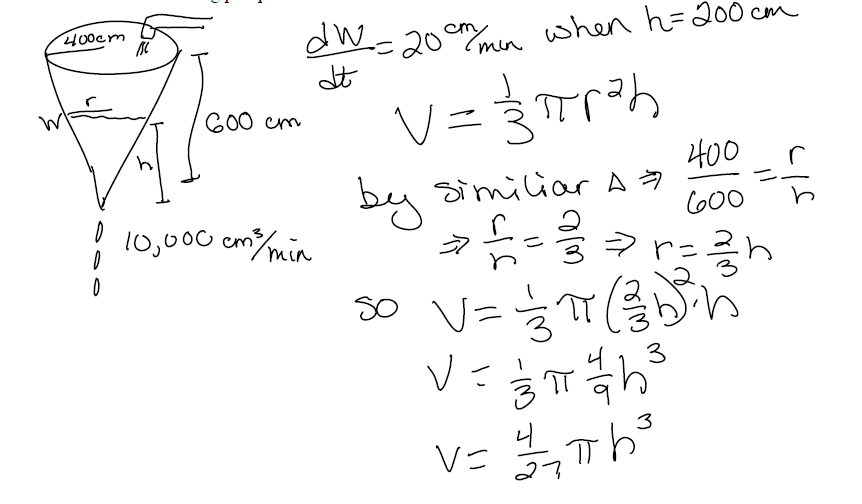
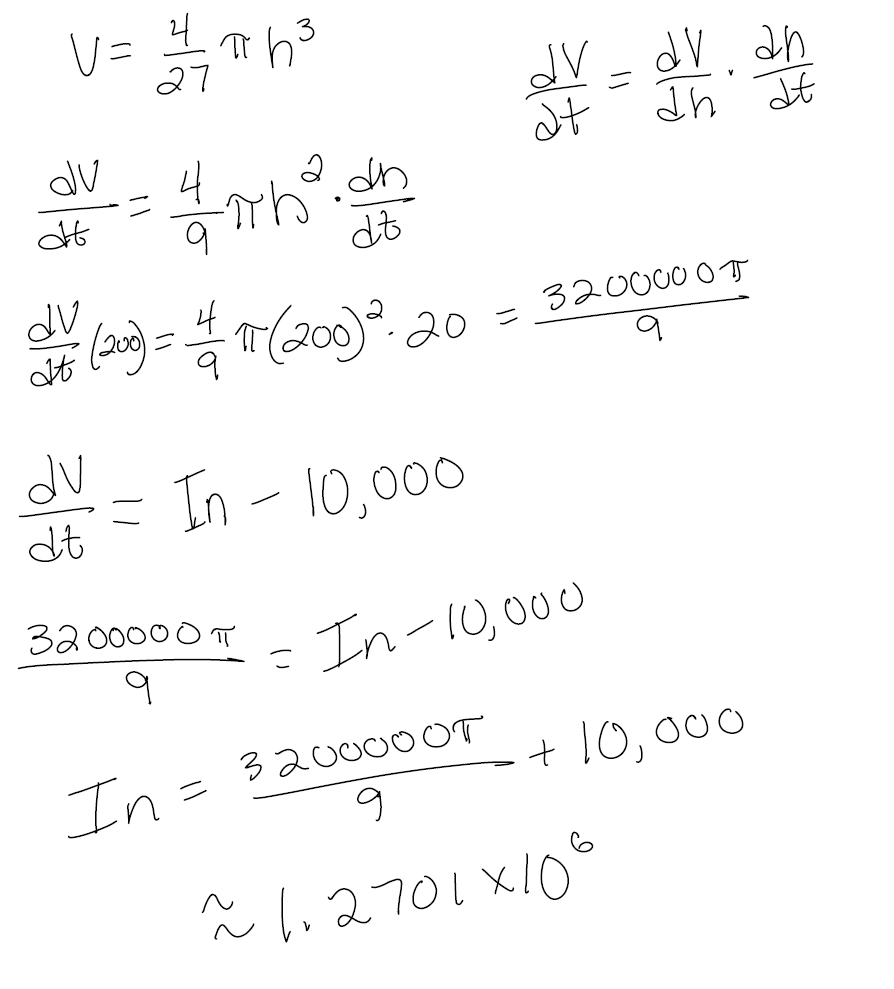
| Prev | Next |