Solutions to graded problems
Section 3.2
2. Using long division:
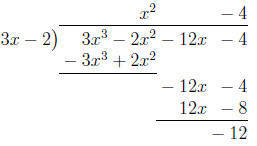
So P(x) = (3x-2)(x2-4)-12.
10. Write P(x) = 2x3-10x2-28x+60.
Then we are told that x =-3 is a solution of the
equation P (x) = 0, which means that (x + 3) must be a factor of P(x), by
the factor
theorem. We use long division to factor P:
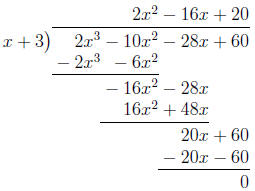
So now the original equation is equivalent to
2(x + 3)(x2-8x + 10) = 0
(I pulled out a 2 for convenience.) To find the remaining two solutions of this
equation
(apart from x =-3), we can use the quadratic formula on the second bracket:
(x2-8x + 10) = 0⇔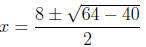 ⇔
⇔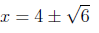
So the equation has solutions x =-3, x = 4-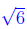 and
x = 4 +
and
x = 4 +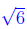 .
.
16. We're told to use a graph to solve the equation x3-3x2-4x+12
= 0. This corresponds
to looking for x- intercepts of the graph y=x3-3x2-4x+12,
sketched below:
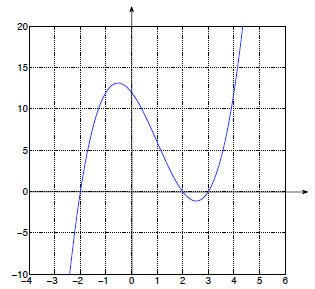
From here, we can immediately read o that the x-intercepts are at (-2,0), (2,0)
and (3,0). By the factor theorem , this means we can write x3-3x2-4x+12=
(x-3)(x-2)(x + 2). So the original equation has solutions x =-2, x = 2 and x =
3.
28. How do we solve a cubic equation such as this one?
First, collect all terms to one side:
x3 + 10x2 + 14x-60 = 0
From this point, our strategy is to inspect the graph and try to find at least one
x -
intercept with rational coordinates (this is what we will do in general, for a
polynomial
equation with degree≥3). The graph is sketched below:
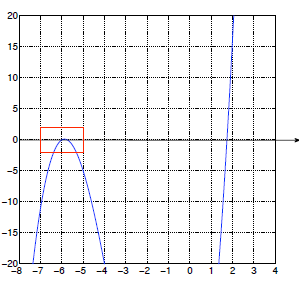
On your calculators, you should use the calculate function to find the
x-intercepts
(carefully!) I have drawn a zoomed -in graph (below) to show what happens near
x =-6.
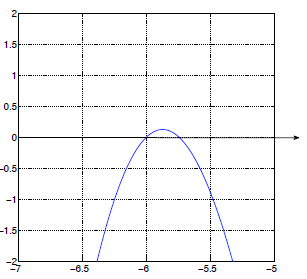
From your calculator, you should find that the x-intercepts are at x =-6, x≈
-5.741657...and x≈1.741657...Obviously, the latter two are not exact . To find
them exactly, we can factor our polynomial, using the information that x =-6 is
an
exact zero:
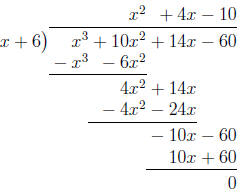
So x3-3x2-4x+12= 0 , (x+6)(x2 +4x-10) = 0 )⇒x
=-6 or x =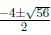 ,
,
So the final, exact solutions are x =-6, x =-2-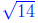 and
x =-2 +
and
x =-2 +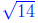
60. The information about the zeros gives that P(x) =
a(x-1)2(x + 1)2. a is a stretching
factor that will be determined by the other piece of information: P(2) = 4 , 4 =
a(1)2(3)2 = 9a⇔a =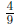 .So
P(x) =
.So
P(x) =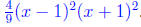 .
.
62. The graph shows that the polynomial P has zeros at x
=-5, x = 2 and x = 5 (all
multiplicity one ), so we immediately have that P(x) = a(x-5)(x-2)(x + 5) (by the
factor theorem). To find the stretch factor a, we use one other point on the
graph: in
this case, the y-intercept (0,50): P(0) = 50⇔50 = a(-5)(-2)(5) = 50a⇔a =
1. So P(x) = (x-5)(x-2)(x + 5).
| Prev | Next |