Systems of Linear Equations and Ax=b
| Outline: 1) The relationship between systems of linear equations and Linear Combinations of vectors 2) The relationship between systems of equations and 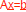 3) Basic rules of Matrix - vector products 4) 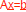 : the fundamental issues : the fundamental issues5) Solving linear systems: Introduction to Gaussian Elimination |
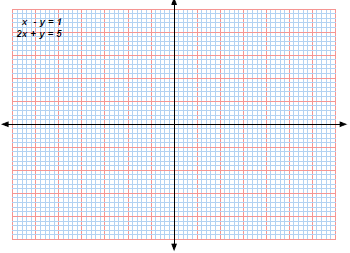
Systems of linear Equations A simple example : x - y = 1 2x + y = 5 Solution by "elimination" and "back-substitution": |
||
| The geometry of Linear Systems: the "row"
picture
|
The geometry of Linear Systems:
the "column" picture Linear systems of equations as Linear Combinations of vectors x - y = 1 |
||
| The geometry of Linear Systems: the "column"
picture
|
3x3 problems (3 equations, 3 unknowns ): | ||
| A more compact approach: Introducing the Matrix A x - y = 1 2x + y = 5 2x2 problem: 3x3 problem: |
Matrix-Vector Products:
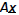 the Column Picture: Example: |
||
Matrix-Vector Products:
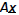 the Row Picture (dot products): Example: Point!: Both Column and Row approaches are identical |
Matrix Component Notation: Matrices in Matlab: |
||
| Big Points: 1) 2) 3) 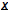 to a new vector to a new vector
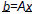 The Forward Problem: you know A and 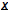 ,
just find ,
just find 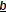 . .Easy! Just use Matrix Vector multiplication . A solution must always exist. The Inverse Problem: Given A and 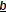 ,
find ,
find 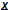 , such that , such that
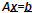 Much Harder! This is the problem of solving linear systems. Fundamental Math questions : Given square A and a vector 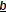 1) does a solution 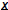 exist such that exist such that
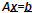 ? ?2) is the solution 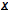 unique ? unique ?3) How do you find 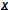 ? ? |
The geometry of
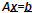
|
||
The geometry of
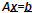 : Interesting complications... : Interesting complications...
|
General results (to be shown): for square nxn A: 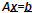 has exactly one of
three outcomes has exactly one of
three outcomes1) There is a unique solution 2) There is no solution 3) There are an infinite number of solutions Question: How can you tell and how do you find the solution? |
||
| Gaussian Elimination: A systematic algorithm to both diagnose and solve linear systems 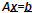 Consider our toy 2x2 problem again:
Suppose you wanted to eliminate x instead of y in
2nd equation? |
Gaussian Elimination: A systematic algorithm to transform a general matrix A to upper Triangular form. 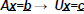 Upper Triangular system: Easily solved by Back Substitution : |
||
| Gaussian Elimination: A systematic algorithm to transform a general matrix A to upper Triangular form. 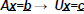 Need to transform both A and the RHS b to maintain equality. Useful to Consider the Augmented matrix 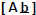 Idea of Elimination: Use row operations to zero out elements below the pivot using multipliers of the pivot row |
Gaussian Elimination: A systematic algorithm to transform a general matrix A to upper Triangular form.  Examples: If it "works", Gaussian Elimination transforms A→U with n distinct pivots. n Pivots implies a unique solution. |
||
| Failure of Gaussian Elimination: Consider: |
Temporary Failure of Gaussian
Elimination: Consider: The Fix: Row exchange (permutation operation |
||
| Gaussian Elimination on a 3x3 system of
equations: Consider: 2x + y + 3z = 3 |
|||
| Gaussian Elimination on a 3x3
system of equations: Example 2 (row exchange): x + 2y + 4z = 1 2x + 4y + 2z = 2 6x + 10y - z = 8 Matrix Vector form: Augmented Matrix form: |
|||
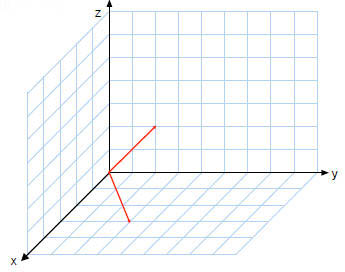
| Gaussian Elimination: The Overall Pattern | Linear combinations in 3 Dimensions
|
||
 |
 |
||
 |
| Prev | Next |