The Cubic Formula
In college algebra we make frequent use of the quadratic
formula . Namely, if
f(x) = ax2 + bx + c,
then the zeroes of f (x) are
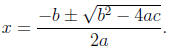
This formula can be derived by completing the square. Note that if b2 − 4ac
(what we call
the discriminant) is negative , then the quadratic polynomial f (x) has two
complex roots.
Otherwise, you get two real roots , and in this case you don’t need to know
anything about
complex numbers .
It is shown in upper-division math that any degree-n polynomial with rational
(or real, or
complex) coefficients has n complex roots. (This fact is called the fundamental
theorem of
algebra.) So, if we have a quadratic formula for finding both (possibly complex)
roots of a
quadratic (degree-2) polynomial, then it’s natural to ask for a formula for all
three roots of a
cubic. Likewise, we would like a formula for all four roots of a quartic, and so
on. It can be
proved (the terms are Galois theory and solvable groups ), that there cannot
exist a general
formula for degree 5 and above.
Here is a presentation of the cubic formula , adapted from Grove’s Algebra. Note
the following:
• It turns out that deriving this formula takes a bit more work. Details are on
pages
278-279 of the reference provided below.
• The formula uses complex numbers. Even if the cubic polynomial has three real
roots,
some intermediate numbers in the formula are complex.
• To use the quadratic formula, you just plug in your coefficients. The cubic
formula, by
contrast, comes in separate steps.
• These days, it’s probably easier to just do graphical
root -finding using your calculator.
However, it’s interesting to see what people did in the old days. (The cubic
formula was
discovered in Renaissance Italy — for example, search Wikipedia for Nicolo
Tartaglia
or Scipio del Ferro).
This formula works for any cubic. At each step of the general procedure, I’ll
also do that
step for a particular example cubic polynomial.
Step 1. Divide the cubic polynomial by its leading coefficient. For example, if
you have
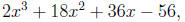
then divide by the leading 2 to obtain
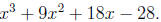
Now you have something of the form
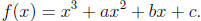
Step 2. It turns out that it is desirable to get rid of one of the coefficients.
To accomplish
this, substitute
x = y − a/3
into f(x) and call the result g(y). For example, using f(x) as above, a = 9 so
a/3 = 3.
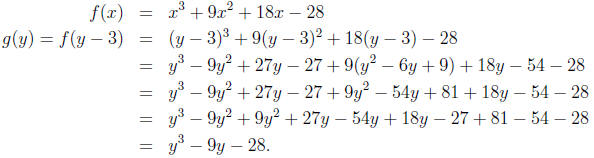
Step 3. Now that we’ve eliminated the quadratic term, we have something of the
form
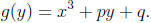
The next step is computing the discriminant of g(y). All polynomials have
discriminants,
but it’s particularly easy to compute now that we have only two coefficients , p
and q. This
is
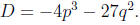
In our example, since we have
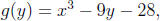 we have
p = −9 and q = −28. So
we have
p = −9 and q = −28. So
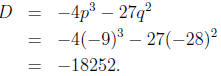
Step 4. Below we’ll need the numbers
−q/2 and 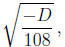
so let’s go ahead and compute them now. In our example, these are
−q/2 = 14 and 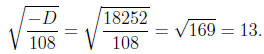
Step 5. Here is the formula for the three roots of the cubic g(y):
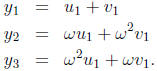
We need to know what 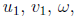 and
and
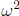 are. First,
are. First,
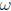 and
and 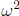 are constants:
are constants:
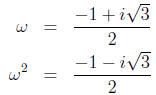
(Side note: 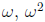 , and 1 are the three complex numbers whose cube is 1. Try FOILing out
, and 1 are the three complex numbers whose cube is 1. Try FOILing out
the product 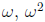 .) Also,
.) Also,
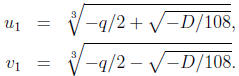
In our example, we have
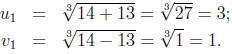
So the first root is
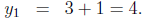
The second root is
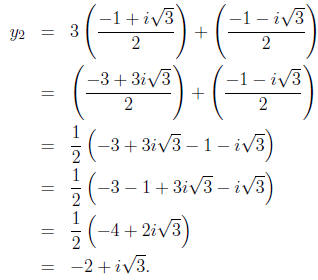
The third root is
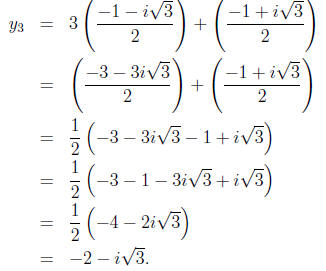
Step 6. We just found the roots of g(y). To finish up, we need to undo the
change of
variable
x = y − a/3.
In our example, we found
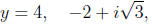 and
and 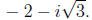
Since a/3 was 3, we have, for the original polynomial
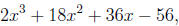
the three roots
 and
and 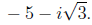
| Prev | Next |