The Real Number System
Please complete your responses to the questions 1-6 at the end of the page on a separate piece of paper.
In mathematics different types of numbers are grouped
together and given names. It is important to have a feeling
for this organization. Consider the following definitions:
The sets of numbers:
| Names | Sets | Notes and examples |
| natural numbers |
{1, 2, 3, . . .} | 1. See note 1. on set notation below: |
| whole numbers |
{0, 1, 2 , 3, . . .} | |
| integers | {0, ±1, ±2, ±3,. . .} | |
| rational | { p/q | p and q are integers, q≠0} |
 |
| real | {x | x can be written as a decimal} |
3 |
| irrational | {x | x is a nonrepeating and nonterminating decimal} |
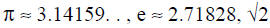 |
Notes:
1. The definitions above are written in set notation. The
{} symbols called braces indicate the closing and
opening of a set or collection of numbers. The three dots after the three
indicate that the pattern continues.
See page 47 in your workbook for more examples.
2. Read as the fraction p over q, where p and q are both integers.
Rational numbers can be written in decimal form , but they always end or
repeat.
3. Read as all numbers x, such that x can be written as a decimal.
Look at the list of numbers. What do you notice? Notice that as you go
down the list a new set will
contain the set of numbers above it. For example, the whole numbers contain the
natural numbers. In fact, the
whole numbers are the natural with one new number, zero. As you go down the list
the numbers get more
"complicated." The progression of numbers is much the way we learn about numbers
as we grow up. We start as
small children with the natural numbers when we count our fingers and toys. Then
we make an intellectual leap
and learn about "all gone" and the concept of zero , which takes us to the whole
numbers. Then at some time in
our development we learn about debt and negative numbers, and we start to use
integers. The same sort of
progression happens in math classes. You start doing math with whole numbers,
then you learn about operation
with negative and positives, and then fractions. Notice the integers are
completely contained by the rational
numbers. Any integer can be written as a rational by putting a one under it. The
one exception to this progression
is the irrational numbers. They are one their own. The rationals and the
irrationals are disjoint sets, which means
you are one, but not the others. These two sets together make the real numbers ,
which we will use in this class.
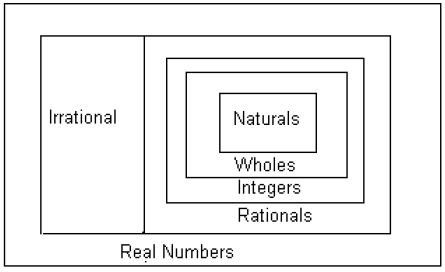
Here is a diagram to help you visualize the sets of numbers.
The real number system consists of two subsets of
numbers, the rational numbers and the irrational numbers.
Contained within the rational numbers are other useful subsets of numbers. The
subsets of real numbers are
nested as indicated by the picture below:
Questions
1. Determine if the following statements are true or false
and give a short reason why:
a. Every integer is a rational number.
b. Every rational number is an irrational number.
c. Every natural number is an integer.
d. Every integer is a natural number.
2. Consider the following set of numbers:
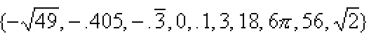
List all the following:
a) natural numbers:
b) whole numbers:
c) integers:
d) rational numbers:
e) irrational numbers:
f) real numbers:
3. Real numbers are ordered . Each real number corresponds
to a point on a line. Using 0 as the middle point,
draw a number line and label the points 2,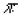 ,
-11/32, 0.
,
-11/32, 0.
4. The following set of numbers, called a data set shows
the projections (in thousands) for the five occupations
with the greatest increase and greatest decrease in jobs from 1984-2005.
| Farmers | Cashiers | Typists | janitorial | Book keeping |
Bank Tellers |
Garment | Retail sales |
Food service |
Nursing |
| -273 | 526 | -212 | 559 | -178 | -152 | -140 | 532 | 479 | 473 |
a. What basic set of numbers does this data belong to?
b. What industry is projected to grow the most?
c. Does the total number of jobs increase or decrease over the period indicated?
d. What is the average amount of increase or decrease in jobs over the time
period indicated? (Round
your answer to a whole number but remember that the original data is in
thousands.)
5. The following data set represents the mass in grams of
various U.S. coins.
| Dime | Penny | Nickel | Quarter | Half- dollar |
Dollar |
| 2.264 | 3.110 | 4.999 | 5.669 | 11.500 | 26.730 |
a. What basic set of numbers does this data belong to?
b. What is the average mass of these coins?( represent your answer to the
nearest ten
thousandth).
c. Why do you think these values are represented to the thousandth place?
6.
In Activity 1, The spiral of Roots, we constructed line segments in
units of inches . Many of the lengths
were irrational: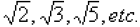 (note that
(note that
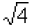 = 2 is rational).
= 2 is rational).
a. What makes an irrational number different from a
rational number?
b. Suppose we want to approximate the value of
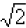 using a rational number written in decimal
form.
using a rational number written in decimal
form.
We would start by observing that 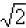 is the
number, a, whose square is 2. Which number below
is the
number, a, whose square is 2. Which number below
would you say is closest to the value of 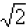 ?
?
| a | 1 | 1.3 | 1.4 | 1.5 | 2 |
| a^2 | 1 | 1.69 | 1.96 | 2.25 | 4 |
c. Evaluating 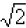 with a calculator results in
the number 1.41421356237. Explain why this is not the
with a calculator results in
the number 1.41421356237. Explain why this is not the
same as 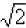 .
.
Answers for Real Numbers and Data Sets
For this activity the Complex number set was disregarded.
1. (a) True (b) False (c) True (d) False
2. Note that 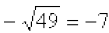
(a) 3,18,56
(b) 0,3,18,56
(c) -7,0,3,18,56
(d) -7,-.405,-.3,0,.1,3,18,56
(e) 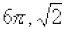
(f) all
3.
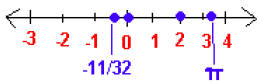
4. (a) integers
(b) janitorial
(c) There will be an overall increase of 1614 thousand jobs, or 1,614,000 jobs
(d) 161 jobs
5. (a) rationals
(b) 9.045 grams
(c) A thousandth of a gram is possibly the level of accuracy required by the
treasury department for minting coins.
6.
(a) An irrational number can not be represented as a fraction. It can be
approximated by a non-repeating non-terminating
decimal. Rational numbers can be represented as fractions which can be converted
to either
repeating or terminating decimals .
(b) 1.4
(c) It is only an approximation, but it is accurate to the hundred billionths
place.
| Prev | Next |