Trigonometric Equations
Objectives
Upon completion of this lesson, you will be able to:
• Solve trigonometric equations over the set of real numbers or on a given
interval.
Required Reading
Swokowski/Cole: Section 6.2, pages 468-479.
Discussion
A trigonometric equation is simply an equation involving trigonometric
functions. We apply the
same methods of solution (such as factoring) to trigonometric equations as we do
to ordinary
equations.
Do not divide by any expression which could be zero.
Example 1: Solve sin2 x = sin x on the interval [0, 2π).
Solution:
It is tempting to divide both sides of the equation by the
factor sin x .
If this is done, we have sin x = 1 and 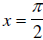 .
.
But in dividing by sin x , we divided by an unknown quantity that may be equal
to 0 and
we lost valid solutions.
The correct solution is as follows :
sin2 x = sin x
sin2 x - sin x = 0  subtract sin x from both
sides
subtract sin x from both
sides
sin x(sin x -1) = 0  factor
factor
sin x = 0 or sin x -1= 0  set each factor
equal to 0 and solve
set each factor
equal to 0 and solve
 sin x = 1
sin x = 1
Hence x = 0,π,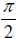
Example 2: Solve 2cos2 x = 1+ sin x on the interval [0, 2π).
Solution: This equation will be quadratic in form once we put it in terms of one
trigonometric
function. We know that cos2 x + sin2 x = 1, so cos2 x = 1- sin2 x .
| 2(1- sin2 x) = 1+ sin x | substitute |
| 2sin2 x + sin x -1 = 0 | write in quadratic form |
| (2sin x -1)(sin x +1) = 0 | factor |
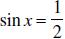 or sin x = -1 or sin x = -1 |
set each factor equal to 0 and solving for sin x |
This gives us the following 3 solutions on the interval
[0, 2π): 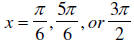
For trigonometric equations that do not factor, use the quadratic formula . The
next
example demonstrates how to handle such a case.
Example 3: Approximate to the nearest 0.1° the solutions on the interval [0°,
360°) for the
equation 2sin2θ - 5sinθ +1 = 0.
Solution: Quadratic Formula: 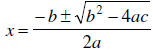
Since the equation is in quadratic form, ax2 + bx + c = 0, with x = sinθ, and a
= 2, b = -5,
and c = 1, we have
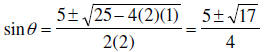
sinθ = 2.2807764064 or sinθ = 0.219223593596
The equation sinθ = 2.2807764064 has no solutions, since -1< sinθ < 1
for all θ.
For sinθ = 0.219223593596, two solutions exist on the interval [0°, 360°],
one in
quadrant I and the other in quadrant II where sinθ > 0.
To find the solutions, set your calculator to degree mode and θ =
sin-1(0.219223593596) .
Hence, the reference angle is 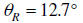
The two solutions are:
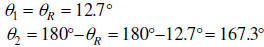
Notes:
(1) Before factoring, be sure the expression is set equal
to zero .
(2) Remember that -1< sinθ < 1 and -1 < cosθ < 1. This will help you
recognize
extraneous values
Practice Problems
Work these problems. Answers to the odd numbered problems can be found at the
end of your
text, even answers are below.
| Section | Pages | Exercises |
| 6.2 | 479-480 | 1, 3, 5, 7, 9, 11, 15, 19, 21, 23, 27, 31, 37,
39, 41, 42, 43, 45, 47, 49, 51, 61, 62, 63, 65, 66 (answer to the nearest 0.1° for 61, 62, 63, 65, 66) |
Answers to even exercises.
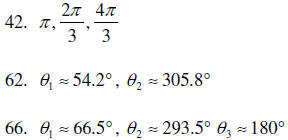
| Prev | Next |